
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏΨ≠Ιΐ‘≠ΒψoΚΆx÷α…œ“ΜΒψAΘ®4Θ§0Θ©Θ§≈ΉΈοœΏΕΞΒψΈΣEΘ§ΥϋΒΡΕ‘≥Τ÷α”κx÷αΫΜ”ΎΒψDΘ°÷±œΏy=©¹2x©¹1Ψ≠Ιΐ≈ΉΈοœΏ…œ“ΜΒψBΘ®©¹2Θ§mΘ©«“”κy÷αΫΜ”ΎΒψCΘ§”κ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΫΜ”ΎΒψFΘ°
Θ®1Θ©«σmΒΡ÷ΒΦΑΗΟ≈ΉΈοœΏΕ‘”ΠΒΡΫβΈω ΫΘΜ
Θ®2Θ©PΘ®xΘ§yΘ© «≈ΉΈοœΏ…œΒΡ“ΜΒψΘ§»τSΓςADP=SΓςADCΘ§«σ≥ωΥυ”–ΖϊΚœΧθΦΰΒΡΒψPΒΡΉχ±ξΘΜ
Θ®3Θ©ΒψQ «ΤΫΟφΡΎ»Έ“β“ΜΒψΘ§ΒψM¥”ΒψF≥ωΖΔΘ§―ΊΕ‘≥Τ÷αœρ…œ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘»ΥΌ‘ΥΕ·Θ§…ηΒψMΒΡ‘ΥΕ· ±ΦδΈΣtΟκΘ§ «ΖώΡή Ι“‘QΓΔAΓΔEΓΔMΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘ°»τΡήΘ§«κ÷±Ϋ”–¥≥ωΒψMΒΡ‘ΥΕ· ±ΦδtΒΡ÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©3Θ§![]() ΘΜΘ®2Θ©P1Θ®
ΘΜΘ®2Θ©P1Θ®![]() Θ§1Θ©Θ§P2Θ®
Θ§1Θ©Θ§P2Θ®![]() Θ§1Θ©Θ§P3Θ®2Θ§©¹1Θ©ΘΜΘ®3Θ©t1=
Θ§1Θ©Θ§P3Θ®2Θ§©¹1Θ©ΘΜΘ®3Θ©t1=![]() Θ§t2=6Θ§t3=
Θ§t2=6Θ§t3=![]() Θ§t4=6.5Θ°
Θ§t4=6.5Θ°
ΓΨΫβΈωΓΩ
‘ΧβΖ÷ΈωΘΚΘ®1Θ© Ήœ»«σ≥ωΒψBΒΡΉχ±ξΚΆmΒΡ÷ΒΘ§»ΜΚσάϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΓςADP”κΓςADC”–Ι≤Ά§ΒΡΒΉ±ΏADΘ§“ρΈΣΟφΜΐœύΒ»Θ§Υυ“‘AD±Ώ…œΒΡΗΏœύΒ»Θ§Φ¥ΈΣ1ΘΜ¥”ΕχΒΟΒΫΒψPΒΡΉίΉχ±ξΈΣ1Θ§‘Όάϊ”Ο≈ΉΈοœΏΒΡΫβΈω Ϋ«σ≥ωΒψPΒΡΉίΉχ±ξΘΜ
Θ®3Θ©»γΫβ¥πΆΦΥυ ΨΘ§‘ΎΒψMΒΡ‘ΥΕ·Ιΐ≥Χ÷–Θ§“ά¥Έ≥ωœ÷ΥΡΗωΝβ–ΈΘ§ΉΔ“β≤Μ“Σ¬©ΫβΘ°’κΕ‘ΟΩ“ΜΗωΝβ–ΈΘ§Ζ÷±πΫχ––ΦΤΥψΘ§«σ≥ωœΏΕΈMFΒΡ≥ΛΕ»Θ§¥”ΕχΒΟΒΫ‘ΥΕ· ±ΦδtΒΡ÷ΒΘ°
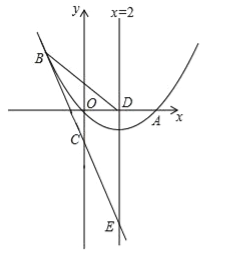
‘ΧβΫβΈωΘΚΘ®1Θ©ΓΏΒψBΘ®©¹2Θ§mΘ©‘Ύ÷±œΏy=©¹2x©¹1…œΘ§Γύm=©¹2ΓΝΘ®©¹2Θ©©¹1=4©¹1=3Θ§Υυ“‘Θ§ΒψBΘ®©¹2Θ§3Θ©Θ§”÷ΓΏ≈ΉΈοœΏΨ≠Ιΐ‘≠ΒψOΘ§Γύ…η≈ΉΈοœΏΒΡΫβΈω ΫΈΣy=ax2+bxΘ§ΓΏΒψBΘ®©¹2Θ§3Θ©Θ§AΘ®4Θ§0Θ©‘Ύ≈ΉΈοœΏ…œΘ§Γύ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ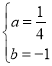 Θ§Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ
Θ§Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() Θ°
Θ°
Θ®2Θ©ΓΏPΘ®xΘ§yΘ© «≈ΉΈοœΏ…œΒΡ“ΜΒψΘ§ΓύPΘ®xΘ§![]() Θ©Θ§»τSΓςADP=SΓςADCΘ§ΓΏSΓςADC=
Θ©Θ§»τSΓςADP=SΓςADCΘ§ΓΏSΓςADC=![]() ADOCΘ§SΓςADP=
ADOCΘ§SΓςADP=![]() AD|y|Θ§”÷ΓΏΒψC «÷±œΏy=©¹2x©¹1”κy÷αΫΜΒψΘ§ΓύCΘ®0Θ§©¹1Θ©Θ§ΓύOC=1Θ§Γύ|
AD|y|Θ§”÷ΓΏΒψC «÷±œΏy=©¹2x©¹1”κy÷αΫΜΒψΘ§ΓύCΘ®0Θ§©¹1Θ©Θ§ΓύOC=1Θ§Γύ|![]() |=1Θ§Φ¥
|=1Θ§Φ¥![]() =1Μρ
=1Μρ![]() =©¹1Θ§ΫβΒΟΘΚx1=
=©¹1Θ§ΫβΒΟΘΚx1=![]() Θ§x2=
Θ§x2=![]() Θ§x3=x4=2Θ§ΓύΒψPΒΡΉχ±ξΈΣ P1Θ®
Θ§x3=x4=2Θ§ΓύΒψPΒΡΉχ±ξΈΣ P1Θ®![]() Θ§1Θ©Θ§P2Θ®
Θ§1Θ©Θ§P2Θ®![]() Θ§1Θ©Θ§P3Θ®2Θ§©¹1Θ©ΘΜ
Θ§1Θ©Θ§P3Θ®2Θ§©¹1Θ©ΘΜ
Θ®3Θ©Ϋα¬έΘΚ¥φ‘ΎΘ°»γΆΦ2
ΓΏ≈ΉΈοœΏΒΡΫβΈω ΫΈΣ![]() Θ§ΓύΕΞΒψEΘ®2Θ§©¹1Θ©Θ§Ε‘≥Τ÷αΈΣx=2ΘΜ
Θ§ΓύΕΞΒψEΘ®2Θ§©¹1Θ©Θ§Ε‘≥Τ÷αΈΣx=2ΘΜ
ΒψF «÷±œΏy=©¹2x©¹1”κΕ‘≥Τ÷αx=2ΒΡΫΜΒψΘ§ΓύFΘ®2Θ§©¹5Θ©Θ§DF=5Θ°
”÷ΓΏAΘ®4Θ§0Θ©Θ§ΓύAE=![]() Θ°
Θ°
»γ”“ΆΦΥυ ΨΘ§‘ΎΒψMΒΡ‘ΥΕ·Ιΐ≥Χ÷–Θ§“ά¥Έ≥ωœ÷ΥΡΗωΝβ–ΈΘΚ
ΔΌΝβ–ΈAEM/span>1Q1Θ°
ΓΏ¥Υ ±EM1=AE=![]() Θ§ΓύM1F=DF©¹DE©¹DM1=
Θ§ΓύM1F=DF©¹DE©¹DM1=![]() Θ§Γύt1=
Θ§Γύt1=![]() ΘΜ
ΘΜ
ΔΎΝβ–ΈAEOM2Θ°
ΓΏ¥Υ ±DM2=DE=1Θ§ΓύM2F=DF+DM2=6Θ§Γύt2=6ΘΜ
ΔέΝβ–ΈAEM3Q3Θ°
ΓΏ¥Υ ±EM3=AE=![]() Θ§ΓύDM3=EM3©¹DE=
Θ§ΓύDM3=EM3©¹DE=![]() ©¹1Θ§ΓύM3F=DM3+DF=Θ®
©¹1Θ§ΓύM3F=DM3+DF=Θ®![]() ©¹1Θ©+5=
©¹1Θ©+5=![]() Θ§Γύt3=
Θ§Γύt3=![]() ΘΜ
ΘΜ
ΔήΝβ–ΈAM4EQ4Θ°
¥Υ ±AEΈΣΝβ–ΈΒΡΕ‘Ϋ«œΏΘ§…ηΕ‘Ϋ«œΏAE”κM4Q4ΫΜ”ΎΒψHΘ§‘ρAEΓΆM4Q4Θ§ΓΏ“Ή÷ΣΓςAEDΓΉΓςM4EHΘ§Γύ![]() Θ§Φ¥
Θ§Φ¥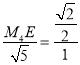 Θ§ΒΟM4E=2.5Θ§ΓύDM4=M4E©¹DE=2.5©¹1=1.5Θ§ΓύM4F=DM4+DF=1.5+5=6.5Θ§Γύt4=6.5Θ°
Θ§ΒΟM4E=2.5Θ§ΓύDM4=M4E©¹DE=2.5©¹1=1.5Θ§ΓύM4F=DM4+DF=1.5+5=6.5Θ§Γύt4=6.5Θ°
Ήέ…œΥυ ωΘ§¥φ‘ΎΒψMΓΔΒψQΘ§ ΙΒΟ“‘QΓΔAΓΔEΓΔMΥΡΒψΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–ΈΘΜ ±ΦδtΒΡ÷ΒΈΣΘΚt1=![]() Θ§t2=6Θ§t3=
Θ§t2=6Θ§t3=![]() Θ§t4=6.5Θ°
Θ§t4=6.5Θ°




 –Γ―ß―ßœΑΚΟΑο ÷œΒΝ–¥πΑΗ
–Γ―ß―ßœΑΚΟΑο ÷œΒΝ–¥πΑΗ –Γ―ßΆ§≤Ϋ»ΐΝΖΚΥ–ΡΟήΨμœΒΝ–¥πΑΗ
–Γ―ßΆ§≤Ϋ»ΐΝΖΚΥ–ΡΟήΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§ΓœBACΘΫ90ΓψΘ§ADΓΆBC”ΎDΘ§‘ρœ¬Ν–Ϋα¬έ÷–Θ§’ΐ»ΖΒΡΗω ΐΈΣΘ® Θ©Θ° ΔΌABΓΆAC; ΔΎAD”κACΜΞœύ¥Ι÷±; ΔέΒψCΒΫABΒΡ¥ΙœΏΕΈ «œΏΕΈAB; ΔήΒψDΒΫBCΒΡΨύάκ «œΏΕΈADΒΡ≥ΛΕ»; ΔίœΏΕΈABΒΡ≥ΛΕ» «ΒψBΒΫACΒΡΨύάκ; ΔόœΏΕΈAB «ΒψBΒΫACΒΡΨύάκ; ΔΏAD>BD. 
A.2Ηω
B.4Ηω
C.7Ηω
D.0Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥œΊΈΣΝΥ¬δ Β÷–―κΒΡΓΑ«ΩΜυΜίΟώΙΛ≥ΧΓ±Θ§ΦΤΜ°ΫΪΡ≥¥εΒΡΨ”ΟώΉ‘ά¥Υ°ΙήΒάΫχ––ΗΡ‘λΘ°ΗΟΙΛ≥Χ»τ”…ΦΉΕ”ΒΞΕά ©ΙΛ«ΓΚΟ‘ΎΙφΕ® ±ΦδΡΎΆξ≥…ΘΜ»τ““Ε”ΒΞΕά ©ΙΛΘ§‘ρΆξ≥…ΙΛ≥ΧΥυ–ηΧλ ΐ «ΙφΕ®Χλ ΐΒΡ1.5±ΕΘ°»γΙϊ”…ΦΉΓΔ““Ε”œ»ΚœΉω15ΧλΘ§Ρ«Ο¥”ύœ¬ΒΡΙΛ≥Χ”…ΦΉΕ”ΒΞΕάΆξ≥…ΜΙ–η5ΧλΘ°
Θ®1Θ©’βœνΙΛ≥ΧΒΡΙφΕ® ±Φδ «Εύ…ΌΧλΘΩ
Θ®2Θ©“―÷ΣΦΉΕ”ΟΩΧλΒΡ ©ΙΛΖ―”ΟΈΣ6500‘ΣΘ§““Ε”ΟΩΧλΒΡ ©ΙΛΖ―”ΟΈΣ3500‘ΣΘ°ΈΣΝΥΥθΕΧΙΛΤΎ“‘Φθ…ΌΕ‘Ψ”Οώ”ΟΥ°ΒΡ”ΑœλΘ§ΙΛ≥Χ÷ΗΜ”≤ΩΉν÷’ΨωΕ®ΗΟΙΛ≥Χ”…ΦΉΓΔ““Ε”ΚœΉωά¥Άξ≥…Θ°‘ρΗΟΙΛ≥Χ ©ΙΛΖ―”Ο «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΒΊ”–ΝΫΗω¥εΉ·MΓΔNΚΆΝΫΧθœύΫΜ≤φΒΡΙΪ¬ΖOAΘ§OBΘ§œ÷ΦΤΜ°–όΫ®“ΜΗωΈοΉ ≤÷ΩβΘ§œΘΆϊ≤÷ΩβΒΫΝΫΗω¥εΉ·ΒΡΨύάκœύΒ»Θ§ΒΫΝΫΧθΙΪ¬ΖΒΡΨύάκ“≤œύΒ»Θ§«κΡψ”Ο≥ΏΙφΉςΆΦΒΡΖΫΖ®»ΖΕ®ΗΟΒψPΘ°Θ®ΉΔ“β±ΘΝτΉςΆΦΚέΦΘΘ§≤Μ”Ο–¥ΉςΖ®Θ©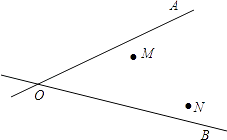
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΉι ΐΨί5Θ§4Θ§2Θ§5Θ§6ΒΡ÷–ΈΜ ΐ «Θ®ΓΓΓΓΘ©
A.5
B.4
C.2
D.6
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–ΥΒΖ®÷–≤Μ’ΐ»ΖΒΡ «Θ® Θ©
A.0 «Ή‘»Μ ΐ
B.0 «’ΐ ΐ
C.0 «’ϊ ΐ
D.0 «Ζ«ΗΚ ΐ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΚλ‘φΖα ’ΝΥΘ§ΈΣΝΥ‘Υ δΖΫ±ψΘ§–ΓΜΣΒΡΑ÷Α÷¥ρΥψΑ―“ΜΗω≥ΛΈΣΘ®a+2bΘ©cmΓΔΩμΈΣΘ®a+bΘ©cmΒΡ≥ΛΖΫ–Έ÷ΫΑε÷Τ≥…“ΜΗω”–ΒΉΈόΗ«ΒΡΚ–Ή”Θ§‘Ύ≥ΛΖΫ–Έ÷ΫΑεΒΡΥΡΗωΫ«ΗςΫΊ»Ξ“ΜΗω±Ώ≥ΛΈΣ ![]() bcmΒΡ–Γ’ΐΖΫ–ΈΘ§»ΜΚσ―Ί’έœΏ’έΤπΦ¥Ω…Θ§»γΆΦΥυ ΨΘ§œ÷ΫΪΚ–Ή”ΒΡΆβ±μΟφΧυ…œ≤ …ΪΜ®ΑεΘ°
bcmΒΡ–Γ’ΐΖΫ–ΈΘ§»ΜΚσ―Ί’έœΏ’έΤπΦ¥Ω…Θ§»γΆΦΥυ ΨΘ§œ÷ΫΪΚ–Ή”ΒΡΆβ±μΟφΧυ…œ≤ …ΪΜ®ΑεΘ° 
Θ®1Θ©‘ρ÷Ν…Ό–η“Σ≤ ÷ΫΒΡΟφΜΐ «Εύ…ΌΘΩ
Θ®2Θ©Β±a=8Θ§b=6 ±Θ§«σ÷Ν…Ό–η“Σ≤ ÷ΫΒΡΟφΜΐ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§ΨΊ–ΈABCDΒΡΝΫΧθ±Ώ‘ΎΉχ±ξ÷α…œΘ§ΒψD”κΉχ±ξ‘≠ΒψO÷ΊΚœΘ§«“AD=8Θ§AB=6Θ°»γΆΦ2Θ§ΨΊ–ΈABCD―ΊOBΖΫœρ“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§Ά§ ±ΒψP¥”AΒψ≥ωΖΔ“≤“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊΨΊ–ΈABCDΒΡ±ΏABΨ≠ΙΐΒψBœρΒψC‘ΥΕ·Θ§Β±ΒψPΒΫ¥οΒψC ±Θ§ΨΊ–ΈABCDΚΆΒψPΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ§…ηΒψPΒΡ‘ΥΕ· ±ΦδΈΣtΟκΘ°

Θ®1Θ©Β±t=5 ±Θ§«κ÷±Ϋ”–¥≥ωΒψDΓΔΒψPΒΡΉχ±ξΘΜ
Θ®2Θ©Β±ΒψP‘ΎœΏΕΈABΜρœΏΕΈBC…œ‘ΥΕ· ±Θ§«σ≥ωΓςPBDΒΡΟφΜΐSΙΊ”ΎtΒΡΚ· ΐΙΊœΒ ΫΘ§≤Δ–¥≥ωœύ”ΠtΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©ΒψP‘ΎœΏΕΈABΜρœΏΕΈBC…œ‘ΥΕ· ±Θ§ΉςPEΓΆx÷αΘ§¥ΙΉψΈΣΒψEΘ§Β±ΓςPEO”κΓςBCDœύΥΤ ±Θ§«σ≥ωœύ”ΠΒΡt÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬Ν–‘ΥΥψ’ΐ»ΖΒΡ «Θ® Θ©
A.©¹a2?Θ®©¹a3Θ©=a6
B.Θ®a2Θ©©¹3=a©¹6
C.Θ® ![]() Θ©©¹2=©¹a2©¹2a©¹1
Θ©©¹2=©¹a2©¹2a©¹1
D.Θ®2a+1Θ©0=1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com