
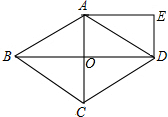
 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,且DE∥AC,AE∥BD.求OE的长.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,且DE∥AC,AE∥BD.求OE的长. 分析 根据菱形的性质得出AC⊥BD,再根据平行四边形的判定定理得四边形AODE为平行四边形,由矩形的判定定理得出四边形AODE是矩形,则该矩形的对角线相等,即AD=OE.
解答  证明:∵四边形ABCD为菱形,
证明:∵四边形ABCD为菱形,
∴AC⊥BD,OA=$\frac{1}{2}$AC=3,OD=$\frac{1}{2}$BD=4,
∴∠AOD=90°,
∴AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵DE∥AC,AE∥BD,
∴四边形AODE为平行四边形,
∴四边形AODE是矩形,
∴OE=AD=5.
点评 本题考查了矩形的判定以及菱形的性质,还考查了平行四边形的判定,掌握平行四边形的判定方法是解题的关键.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:选择题
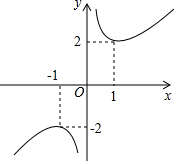 函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )
函数y=x+x-1的图象如图所示,下列对该函数性质的论断不可能正确的是( )| A. | 该函数的图象是中心对称图形 | |
| B. | 当x>0时,该函数在x=1时取得最小值2 | |
| C. | 在每个象限内,y的值随x值的增大而减小 | |
| D. | y的值不可能为1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
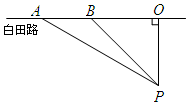 校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.
校车安全是近几年社会关注的热门话题,其中超载和超速行驶是校车事故的主要原因.小亮和同学尝试用自己所学的三角函数知识检测校车是否超速,如下图,观测点设在到白田路的距离为100米的点P处.这时,一辆校车由西向东匀速行驶,测得此校车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
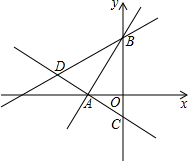 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根.
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
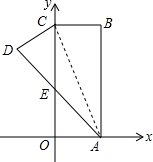 如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为(-$\frac{15}{17}$,$\frac{60}{17}$).
如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为(-$\frac{15}{17}$,$\frac{60}{17}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com