Question

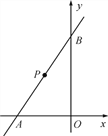
【题目】如图，在平面直角坐标系中，已知直线y＝kx＋6与x轴、y轴分别交于A，B两点，且△ABO的面积为12.

（1）求k的值；

（2）若点P为直线AB上的一动点，P点运动到什么位置时，△PAO是以OA为底的等腰三角形？求出此时点P的坐标；

（3）在（2）的条件下，连接PO，△PBO是等腰三角形吗？如果是，试说明理由；如果不是，请在线段AB上求一点C，使得△CBO是等腰三角形．

Answer 1

【答案】（1） ；（2）P点坐标为（－2，3）；（3）是，理由见解析

【解析】试题分析：（1）令x=0代入y=kx+b得出点B的坐标，根据△ABO的面积易求点A的坐标．把点A的坐标代入解析式求出k值即可； （2）过点P作OA的垂线交OA于点M，连接OP.根据等腰三角形的三线合一的性质推出点P的横坐标，代入解析式可求出点P的纵坐标，从而求出点P的坐标；（3）△PBO是等腰三角形，根据已知条件易证∠ABO=∠POB，即可证得结论．

试题解析：

（1）对于y＝kx＋6，设x＝0，得y＝6.

∴B（0，6），OB＝6.

∵△ABO的面积为12，

∴AO·OB＝12，即AO×6＝12.

解得OA＝4.

∴A（－4，0）．

把A（－4，0）代入y＝kx＋6，得－4k＋6＝0.

解得k＝.

（2）过点P作OA的垂线交OA于点M，连接OP.

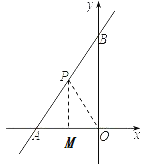
∵PA＝PO，PM⊥OA，

∴OM＝OA＝2.

∴可设P（－2，n）．

把P（－2，n）代入y＝x＋6，得n＝3.

∴P点坐标为（－2，3）．

（3）△PBO是等腰三角形．理由如下：

∵△PAO是以OA为底的等腰三角形，

∴∠PAO＝∠POA.

∵∠PAO＋∠ABO＝90°，∠POA＋∠POB＝90°，

∴∠ABO＝∠POB.

∴PB＝PO.

∴△PBO是等腰三角形．