如图，点P是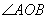
的边OB上的一点．
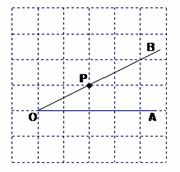
(1)过点P画OB的垂线，交OA于点C；
(2)过点P画OA的垂线，垂足为H；
(3)线段PH的长度是点P到 的距离，线段 的长度是点C到直线OB的距离．因为直线外一点到直线上各点连接的所有线中，垂线段最短，所以线段PC、PH、OC这三条线段大小关系是 ．（用“<”号连接）
科目：初中数学 来源： 题型：
关于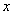
的方程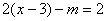
的解和方程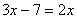
的解相同.
(1) 求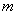
的值；
(2) 已知
线段AB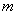＝，在线段AB上取一点P，恰好使AP=2PB，点Q为PB的中点，
求线段AQ的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
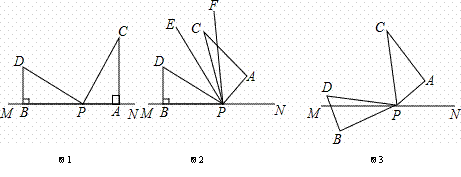
如图，两个形状．大小完全相同的含有30゜、60゜的三角板如图放置，PA、PB与直线MN重合，且三角板PAC，
三角板PBD均可以绕点P逆时针旋转．
（1）试说明：∠DPC=90゜；
（2）如图，若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度，PF平分∠A
PD，PE平分∠CPD，求∠EPF；
（3）如图，若三角板PAC的边PA从PN处开始绕点P逆时针旋转，转速为3゜/秒，同时三角板PBD的边PB从PM处开始绕点P逆时针旋转，转速为2゜/秒，在两个三角板旋转过程中（PC转到与PM重合时，两三角板都停止转动）．设两个三角板旋转时间为t秒，则∠BPN= ，∠CPD= （用含有t的代数式表示，并化简）；以下两个结论：①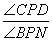
为定值；②∠BPN+∠CPD为定值，正确的是
（填写你认为正确结论的对应序号）．
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
某年级380名师生秋游，计划租用7辆客车，现有甲、乙两种型号客车，它们的载客量和租金如表．
| 甲种客车 | 乙种客车 | |
| 载客量（座/辆） | 60 | 45 |
| 租金（元/辆） | 550 | 450 |
（1）设租用甲种客车x辆，租车总费用为y元．求出y（元）与x（辆）之间的函数表达式；
（2）当甲种客车有多少辆时，能保障所有的师生能参加秋游且租车费用最少，最少费用是多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的值是6，那么代数式
的值是 .
的解满足x+y=2，则d的值为（ ）