
【题目】阅读下面的文字,解答问题
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2)
﹣2)
请解答:
(1)![]() 整数部分是 ,小数部分是 .
整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求|a﹣b|+
的整数部分为b,求|a﹣b|+![]() 的值.
的值.
(3)已知:9+![]() =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长均为1,每个小方格的顶点叫格点
(1)画出△ABC中AB边上的中线CD;
(2)画出△ABC向右平移4个单位后得到的△A1B1C1;
(3)图中AC与A1C1的关系是:______;
(4)S△ABC的面积是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 在数轴上的位置如图所示,所对应的点分别为
在数轴上的位置如图所示,所对应的点分别为![]() .
.
![]()
(1)在数轴上表示![]() 的点与表示
的点与表示![]() 的点之间的距离为 ;由此可得点
的点之间的距离为 ;由此可得点![]() 之间的距离为
之间的距离为
(2)化简:![]()
(3)若![]() 的倒数是它本身,
的倒数是它本身,![]() 的绝对值的相反数是
的绝对值的相反数是![]() ,
,![]() 是数轴上表示
是数轴上表示![]() 的一点,且
的一点,且![]() ,求
,求![]() 所表示的数.
所表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
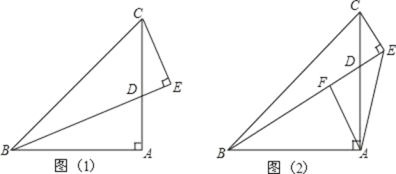
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E是等边△ABC的边BC上一点,以AE为边作等边△AEF,EF交AC于D.
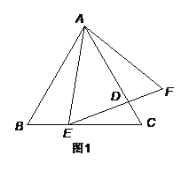
(1)连接CF,求证:![]()
(2)如图2,作EH AF交AB于点H.
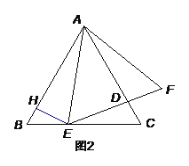
①求证:![]() ;
;
②若EH=2,ED=4,直接写出BE的长为 _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:在数轴上表示两个数![]() 的点之间的距离可以表示为
的点之间的距离可以表示为![]() ,比如表示3的点与-2的点之间的距离表示为
,比如表示3的点与-2的点之间的距离表示为![]() ;
;![]() 可以表示数
可以表示数![]() 的点与表示数1的点之间的距离与表示数
的点与表示数1的点之间的距离与表示数![]() 的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
![]()
(1)解方程![]()
(2)![]() 的最小值是 .
的最小值是 .
(3)![]() 的最小值是 此时
的最小值是 此时![]() 的值为 .
的值为 .
拓展推广:如图所示:当表示数![]() 的点在点
的点在点![]() 和点
和点![]() 之间(包含点
之间(包含点![]() 和点
和点![]() )时,表示数
)时,表示数![]() 的点与点
的点与点![]() 的距离与表示数
的距离与表示数![]() 的点和点
的点和点![]() 的距离之和最小,且最小值为3,即
的距离之和最小,且最小值为3,即![]() 的最小值是3,且此时
的最小值是3,且此时![]() 的取值范围为
的取值范围为
(4)已知数![]() 满足
满足![]() 则
则![]()
(5)当![]() 的最小值是4.5时,求出
的最小值是4.5时,求出![]() 的值及对应
的值及对应![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
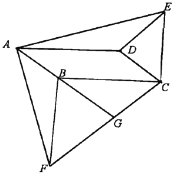
【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com