
【题目】阅读材料:在数轴上表示两个数![]() 的点之间的距离可以表示为
的点之间的距离可以表示为![]() ,比如表示3的点与-2的点之间的距离表示为
,比如表示3的点与-2的点之间的距离表示为![]() ;
;![]() 可以表示数
可以表示数![]() 的点与表示数1的点之间的距离与表示数
的点与表示数1的点之间的距离与表示数![]() 的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
![]()
(1)解方程![]()
(2)![]() 的最小值是 .
的最小值是 .
(3)![]() 的最小值是 此时
的最小值是 此时![]() 的值为 .
的值为 .
拓展推广:如图所示:当表示数![]() 的点在点
的点在点![]() 和点
和点![]() 之间(包含点
之间(包含点![]() 和点
和点![]() )时,表示数
)时,表示数![]() 的点与点
的点与点![]() 的距离与表示数
的距离与表示数![]() 的点和点
的点和点![]() 的距离之和最小,且最小值为3,即
的距离之和最小,且最小值为3,即![]() 的最小值是3,且此时
的最小值是3,且此时![]() 的取值范围为
的取值范围为
(4)已知数![]() 满足
满足![]() 则
则![]()
(5)当![]() 的最小值是4.5时,求出
的最小值是4.5时,求出![]() 的值及对应
的值及对应![]() 的值或取值范围.
的值或取值范围.
【答案】(1)x=-1或x=-3(2)8;(3)5; 0;拓展推广: -2≤x≤1;(4)-9;8;(5)a=3.5,x=0或a=-4.5, x=-1.
【解析】
(1)根据题意及绝对值的含义即可求解;
(2)根据绝对值的几何意义,得出![]() 的最小值;
的最小值;
(3)根据绝对值的几何意义,得出![]() 的最小值及x的值;
的最小值及x的值;
拓展推广:根据绝对值的几何意义,可得![]() 取最小值时,x的取值为-2≤x≤1;
取最小值时,x的取值为-2≤x≤1;
(4)根据![]() 变形得
变形得![]() ,根据题意及绝对值的几何含义得到x,y的取值即可求解;
,根据题意及绝对值的几何含义得到x,y的取值即可求解;
(5)根据题意分a>0和a<-1两种情况分别求解即可.
(1)解![]()
x+2=1或x+2=-1
解得x=-1或x=-3
(2)根据绝对值的几何意义可得,当2≤x≤6时,![]() 的最小值是8
的最小值是8
故答案为:8;
(3)根据绝对值的几何意义可得,当x=0时,![]() 的最小值是5,
的最小值是5,
故答案为:5; 0;
拓展推广:根据绝对值的几何意义可得:当![]() 的最小值是3时,x的取值为-2≤x≤1
的最小值是3时,x的取值为-2≤x≤1
故答案为:-2≤x≤1;
(4)∵![]()
∴![]()
∵![]() 的最小值为10,
的最小值为10,![]() 的最小值为7,
的最小值为7,
根据绝对值的几何含义可得x的取值是-8≤x≤2;y的取值是-1≤x≤6
故当x=-8,y=-1时![]() 的最小值是-9;
的最小值是-9;
故当x=2,y=6时![]() 的最大值是8;
的最大值是8;
故答案为:-9;8;
(5)如图,当a>0时,∵![]() 的最小值是4.5
的最小值是4.5
∴a=4.5-1=3.5,此时x=0
当a<-1时,∵![]() 的最小值是4.5
的最小值是4.5
∴a=0-4.5=-4.5, 此时x=-1.
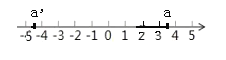


科目:初中数学 来源: 题型:
【题目】某书报亭开设两种租书方式:一种是零星租书,每册收费1元;另一种是会员卡租书,办卡费每月12元,租书费每册0.4元.小军经常来该店租书,若每月租书数量为x册.
(1)写出零星租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式。
(元)与租书数量x(册)之间的函数关系式。
(2)写出会员卡租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式.
(元)与租书数量x(册)之间的函数关系式.
(3)小军选取哪种租书方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2)
﹣2)
请解答:
(1)![]() 整数部分是 ,小数部分是 .
整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a,![]() 的整数部分为b,求|a﹣b|+
的整数部分为b,求|a﹣b|+![]() 的值.
的值.
(3)已知:9+![]() =x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
=x+y,其中x是整数,且0<y<1,求x﹣y的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月第18号台风“泰利”给某地造成严重影响.草根救援队驾若冲锋舟沿一条东西方向的河流营救灾民,早晨从![]() 地出发,晚上最后到达
地出发,晚上最后到达![]() 地,约定向东为正方向,当天航行依次记录如下(单位:千米)
地,约定向东为正方向,当天航行依次记录如下(单位:千米) ![]() 问:
问:
(1)![]() 地在
地在![]() 地的东面,还是西面?与
地的东面,还是西面?与![]() 地相距多少千米?
地相距多少千米?
(2)若冲锋舟每千米耗油0.5升,每升汽油需6.8元,问冲锋舟工作一天需汽油费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
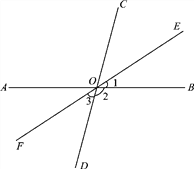
【题目】如图,直线AB、CD相交于点O,∠BOC=80°,OE是∠BOC的角平分线,OF是OE的反向延长线.
(1)求∠2、∠3的度数;
(2)说明OF平分∠AOD的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查适合做抽样调查的是![]()
![]()
A. 检查一枚用于发射卫星的运载火箭的各零部件
B. 对某社区的卫生死角进行调查
C. 对某班学生进行6月5日式“世界环境日”知晓情况的调查
D. 对中学生目前的睡眠情况进行调查
查看答案和解析>>
科目:初中数学 来源: 题型:
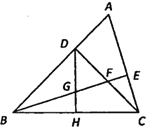
【题目】如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F,H是边BC的中点,连接 DH与 BE相交于点 G,若GE=3,则BF=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
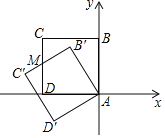
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com