
【题目】已知![]() 的半径为
的半径为![]() ,弦
,弦![]() ,
,![]() ,
,![]() ,则
,则![]() 和
和![]() 的距离为________.
的距离为________.
【答案】14或2
【解析】分两种情况:①当AB、CD在圆心O的两侧时,如图1,作辅助线,构建两个直角三角形,先由垂径定理得出BF和ED的长,再利用勾股定理计算出OE和OF的长,相加即可求出距离EF的长;
②当AB、CD在圆心O的同侧时,如图2,同理求得距离EF的长.
分两种情况:
①当AB、CD在圆心O的两侧时,如图1,过O作OE⊥CD于E,延长EO交AB于F,连接OD、OB,
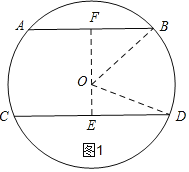
∵AB∥CD,
∴EF⊥AB,
∴ED=![]() CD,BF=
CD,BF=![]() AB,
AB,
∵AB=12,CD=16,
∴ED=![]() ×16=8,BF=
×16=8,BF=![]() ×12=6,
×12=6,
由勾股定理得:OE=![]() ,
,
OF=![]() ,
,
∴EF=OE+OF=6+8=14;
②当AB、CD在圆心O的同侧时,如图2,
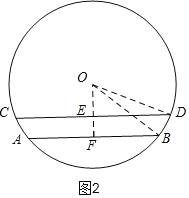
同理得:EF=OF-OE=8-6=2,
综上所述,AB和CD的距离为14或2.


科目:初中数学 来源: 题型:
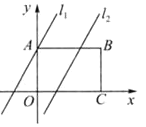
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A,C在坐标轴上,点P在BC边上,直线ι1:y=2x+3,直线ι2:y=2x-3
(1)求直线l1与x轴的交点坐标T,直线ι2与AB的交点坐标Q和与x轴的交点坐标G;
(2)判定四边形ATGQ的形状并求它的面积;
(3)已知点M在第一象限,且是直线l2上的点,若ΔAPM是等腰直角三角形,求点M坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 在数轴上的位置如图所示,所对应的点分别为
在数轴上的位置如图所示,所对应的点分别为![]() .
.
![]()
(1)在数轴上表示![]() 的点与表示
的点与表示![]() 的点之间的距离为 ;由此可得点
的点之间的距离为 ;由此可得点![]() 之间的距离为
之间的距离为
(2)化简:![]()
(3)若![]() 的倒数是它本身,
的倒数是它本身,![]() 的绝对值的相反数是
的绝对值的相反数是![]() ,
,![]() 是数轴上表示
是数轴上表示![]() 的一点,且
的一点,且![]() ,求
,求![]() 所表示的数.
所表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E是等边△ABC的边BC上一点,以AE为边作等边△AEF,EF交AC于D.
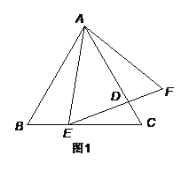
(1)连接CF,求证:![]()
(2)如图2,作EH AF交AB于点H.
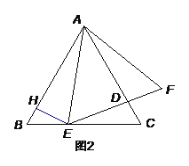
①求证:![]() ;
;
②若EH=2,ED=4,直接写出BE的长为 _________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区一电瓶小客车接到任务从景区大门出发,向东走2千米到达A景区,继续向东走2.5千米到达B景区,然后又回头向西走8.5千米到达C景区,最后回到景区大门.
![]()
(1)以景区大门为原点,向东为正方向,以1个单位长表示1千米,建立如图所示的数轴,请在数轴上表示出上述A、B、C三个景区的位置.
(2)若电瓶车充足一次电能行走15千米,则该电瓶车能否在一开始充好电而途中不充电的情况下完成此次任务?请计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:在数轴上表示两个数![]() 的点之间的距离可以表示为
的点之间的距离可以表示为![]() ,比如表示3的点与-2的点之间的距离表示为
,比如表示3的点与-2的点之间的距离表示为![]() ;
;![]() 可以表示数
可以表示数![]() 的点与表示数1的点之间的距离与表示数
的点与表示数1的点之间的距离与表示数![]() 的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
的点与表示数-2的点之间的距离的和,根据上述材料,回答下列问题:
![]()
(1)解方程![]()
(2)![]() 的最小值是 .
的最小值是 .
(3)![]() 的最小值是 此时
的最小值是 此时![]() 的值为 .
的值为 .
拓展推广:如图所示:当表示数![]() 的点在点
的点在点![]() 和点
和点![]() 之间(包含点
之间(包含点![]() 和点
和点![]() )时,表示数
)时,表示数![]() 的点与点
的点与点![]() 的距离与表示数
的距离与表示数![]() 的点和点
的点和点![]() 的距离之和最小,且最小值为3,即
的距离之和最小,且最小值为3,即![]() 的最小值是3,且此时
的最小值是3,且此时![]() 的取值范围为
的取值范围为
(4)已知数![]() 满足
满足![]() 则
则![]()
(5)当![]() 的最小值是4.5时,求出
的最小值是4.5时,求出![]() 的值及对应
的值及对应![]() 的值或取值范围.
的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠ABC,补充一个条件,使得△ABD≌△ABC,则下列选项不符合题意的是( )
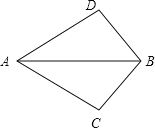
A. ∠D=∠CB. ∠DAB=∠CABC. BD=BCD. AD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为![]() ,宽为
,宽为![]() 的长方形白纸,按图示方法粘合起来,粘合部分宽为
的长方形白纸,按图示方法粘合起来,粘合部分宽为![]() .
.
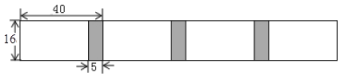
(1)根据图示,将下表补充完整;
白纸张数 | 1 | 2 | 3 | 4 | 5 | … |
纸条长度/ | 40 | 110 | 145 | … |
(2)设![]() 张白纸粘合后的总长度为
张白纸粘合后的总长度为![]() ,求
,求![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)将若干张白纸按上述方式粘合起来,你认为总长度可能为![]() 吗?为什么?
吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com