
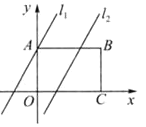
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A,C在坐标轴上,点P在BC边上,直线ι1:y=2x+3,直线ι2:y=2x-3
(1)求直线l1与x轴的交点坐标T,直线ι2与AB的交点坐标Q和与x轴的交点坐标G;
(2)判定四边形ATGQ的形状并求它的面积;
(3)已知点M在第一象限,且是直线l2上的点,若ΔAPM是等腰直角三角形,求点M坐标
【答案】(1)T的坐标为(![]() ,0),Q的坐标为(3,3),G的坐标为(
,0),Q的坐标为(3,3),G的坐标为(![]() ,0);(2)四边形ATGQ是平行四边形,面积为9;(3)点M的坐标为
,0);(2)四边形ATGQ是平行四边形,面积为9;(3)点M的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据坐标轴上的点的坐标特点可求直线l1与x轴的交点坐标T,直线l2与x轴的交点坐标G,根据直线AB上点的纵坐标特征可求直线l2与AB的交点坐标Q;
(2)从四边形ATGQ的两组对边的位置关系和一组邻边的数量关系进行判断即可;
(3)作图分三种情况讨论,设点![]() 的坐标为
的坐标为![]() ,根据证明三角形全等得到对应边长的关系,结合题目数据列出等式,求解x的值即可.
,根据证明三角形全等得到对应边长的关系,结合题目数据列出等式,求解x的值即可.
解:(1)直线l1:当y=0时,2x+3=0,解得![]() ,则直线l1与x轴的交点T的坐标为(
,则直线l1与x轴的交点T的坐标为(![]() ,0);直线l2:当y=3时,2x-3=3,解得x=3,则直线l2与AB的交点Q的坐标为(3,3),当y=0时,2x-3=0,解得
,0);直线l2:当y=3时,2x-3=3,解得x=3,则直线l2与AB的交点Q的坐标为(3,3),当y=0时,2x-3=0,解得![]() ,则直线l2与x轴的交点G的坐标为(
,则直线l2与x轴的交点G的坐标为(![]() ,0).
,0).
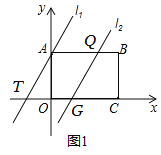
(2)如图1,因为直线l1与直线l2的k相同,都是2,所以AT∥QG,因为T(![]() ,0),G(
,0),G(![]() ,0),所以TG=3≠AT,又因为AB∥OC,所以四边形ATGQ是平行四边形,且平行四边形ATGQ 的面积=TG×OA=3×3=9.
,0),所以TG=3≠AT,又因为AB∥OC,所以四边形ATGQ是平行四边形,且平行四边形ATGQ 的面积=TG×OA=3×3=9.
(3)①若点A为直角顶点,点M在第一象限,AM=AP,如图2,过点P作PF⊥y轴于点F,过点M作MN⊥y轴于点N,则Rt△AMN≌Rt△PAF,∴MN=AF,AN=PF=4,∴M点的纵坐标为7,当y=7时,2x-3=7,解得x=5,即MN=5,∴AF=5,于是P点的坐标为(4,-2),∵点P在BC边上,∴此种情形点M不存在;

②若点P为直角顶点,点M在第一象限,如图3,过点M作MN⊥CB交CB的延长线于点N,
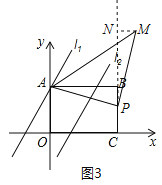
则Rt△ABP≌Rt△PNM,
∴AB=PN=4,MN=BP,
设M(x,2x-3),则MN=x-4,∴![]() ,解得
,解得![]() ,
,![]() ;
;
③若点M为直角顶点时,点M在第一象限,如图4,设![]() ,
,
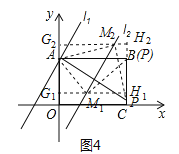
过点![]() 作
作![]() 交OA于点G1,交BC于点
交OA于点G1,交BC于点![]() ,
,
则Rt△AM1G1≌Rt△PM1H1,
∴![]() ,
,
∴![]() ,
,
解得x=2,∴![]() ;
;
设![]() ,同理可得
,同理可得![]() ,解得
,解得![]() ,∴
,∴![]() .
.
综上所述,点M的坐标为![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
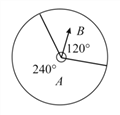
【题目】有一个转盘如图,让转盘自由转动,指针落在分界线重新转动.
(1)让转盘自由转动一次,求落在A区域和落在B区域的概率;
(2)让转盘自由转动两次,求两次都落在A区域的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,将△ABD沿AB向下平移使A点到达B点,得到△BEC,下列说法正确的是( )
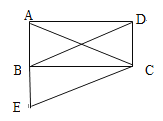
A. △ACE一定是等腰三角形B. △ACE一定是等边三角形
C. △ACE一定是锐角三角形D. △ACE不可能是等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC、BD相交于点O,点E为边CD的中点,若菱形ABCD的周长为16,∠BAD=60°,则△OCE的面积是( )
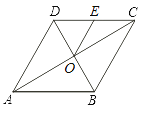
A. ![]() B. 2 C.
B. 2 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“传承好家风”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文中随机抽取了部分参赛征文,统计了他们的成绩,并绘制了如下不完整的两幅统计图表.

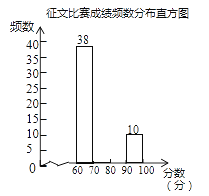
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中c的值是________;
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书报亭开设两种租书方式:一种是零星租书,每册收费1元;另一种是会员卡租书,办卡费每月12元,租书费每册0.4元.小军经常来该店租书,若每月租书数量为x册.
(1)写出零星租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式。
(元)与租书数量x(册)之间的函数关系式。
(2)写出会员卡租书方式应付金额![]() (元)与租书数量x(册)之间的函数关系式.
(元)与租书数量x(册)之间的函数关系式.
(3)小军选取哪种租书方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
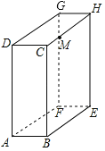
【题目】如图,长方体的长BE=20cm,宽AB=10cm,高AD=15cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com