
 如图甲所示,将一副三角尺的直角顶点重合在点O处.
如图甲所示,将一副三角尺的直角顶点重合在点O处.

科目:初中数学 来源: 题型:
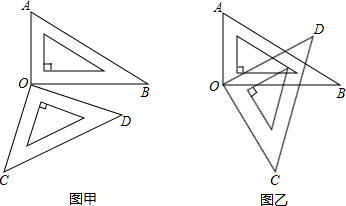
 27、如图甲所示,将一副三角尺的直角顶点重合在点O处.
27、如图甲所示,将一副三角尺的直角顶点重合在点O处.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2014北师大版七年级上册(专题训练 状元笔记)数学:第四章基本平面图形 题型:044
如图甲所示,将一副三角尺的直角顶点重合在点O处.
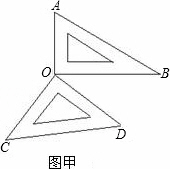
(1)①∠AOD和∠BOC相等吗?说明理由.
②∠AOC和∠BOD在数量上有何关系?说明理由.
(2)若将这幅三角尺按图乙所示摆放,三角尺的直角顶点重合在点O处.
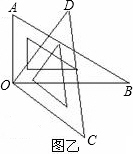
①∠AOD和∠BOC相等吗?说明理由.
②∠AOC和∠BOD的以上关系还成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏期末题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com