
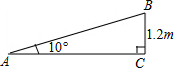
 一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或结论错误的是( )
一个公共房门前的台阶高出地面1.2米,台阶拆除后,换成供轮椅行走的斜坡,数据如图所示,则下列关系或结论错误的是( )| A. | 斜坡AB的坡角是10° | B. | 斜坡AB的坡度是tan10° | ||
| C. | AC=1.2tan10°米 | D. | AB=$\frac{1.2}{sin10°}$米 |
分析 先根据坡度,坡角判断出A,B,再用锐角三角函数判断出C,D即可.
解答 解:根据坡角的定义得,斜坡AB的坡角是10°,此结论正确;即:A正确,
根据坡度的定义得,斜坡AB的坡度是tan10°,此结论正确;即:B正确,
在Rt△ABC中,∠BAC=10°,BC=1.2,
∴tan∠BAC=$\frac{BC}{AC}$=$\frac{1.2}{AC}$,
∴AC=$\frac{1.2}{tan10°}$米,此结论错误,即:C错误;
在Rt△ABC中,∠BAC=10°,BC=1.2,
∴sin∠BAC=$\frac{BC}{AB}$=$\frac{1.2}{AB}$,
∴AB=$\frac{1.2}{sin10°}$米,此结论正确,即:D正确.
故选C.
点评 此题是解直角三角形--坡度坡角问题,主要考查了坡度坡角的定义,解直角三角形,解本题的关键是掌握锐角三角函数的定义.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 若3a>6,则a>2 | B. | 若$-\frac{2}{3}x>1$,则$x<-\frac{2}{3}$ | ||
| C. | 若-x<5,则x>-5 | D. | 若$\frac{1}{3}x<1$,则x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1080° | B. | 900° | C. | 1260° | D. | 1440° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
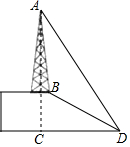 某公司移动电话信号收发塔AB建在学校的科技楼BC上,小飞同学利用测倾器在与点C距离为27米远的点D处测得塔顶A的仰角为60°,塔底B的仰角为30°,则信号收发塔AB的高度约为( )米.(精确到0.1米,$\sqrt{3}≈1.73,\sqrt{5}≈2.24$)
某公司移动电话信号收发塔AB建在学校的科技楼BC上,小飞同学利用测倾器在与点C距离为27米远的点D处测得塔顶A的仰角为60°,塔底B的仰角为30°,则信号收发塔AB的高度约为( )米.(精确到0.1米,$\sqrt{3}≈1.73,\sqrt{5}≈2.24$)| A. | 31.2 | B. | 31.1 | C. | 30.2 | D. | 30.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com