
 如图,一次函数y=-x-1与反比例函数y=$\frac{m}{x}$的图象交于点A,一次函数y=-x-1与坐标轴分别交于B、C两点,连结AO,若tan∠AOB=$\frac{1}{2}$.
如图,一次函数y=-x-1与反比例函数y=$\frac{m}{x}$的图象交于点A,一次函数y=-x-1与坐标轴分别交于B、C两点,连结AO,若tan∠AOB=$\frac{1}{2}$.分析 (1)由点A在一次函数图象上,设出点A的坐标,再根据正切的定义结合tan∠AOB=$\frac{1}{2}$可得出关于n的一元一次方程,解方程即可求出n值,从而得出点A的坐标,再由反比例函数图象上点的坐标特征可求出m的值,此题得解;
(2)根据对称性结合点A的坐标可得出点D的坐标,令一次函数中x=0求出y值,即可得出点C的坐标,由C、D的坐标可得出线段CD∥x轴以及线段CD的长度,再根据三角形的面积公式即可得出结论.
解答 解:(1)∵点A在一次函数y=-x-1的图象上,
∴设点A的坐标为(n,-n-1)(n<0).
∵tan∠AOB=$\frac{-n-1}{-n}$=$\frac{1}{2}$,
解得:n=-2,
∴点A的坐标为(-2,1),
∴m=-2×1=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$.
(2)∵点A的坐标为(-2,1),
∴点D的坐标为(2,-1).
令一次函数y=-x-1中x=0,则y=-1,
∴点C的坐标为(0,-1).
∴线段CD与x轴平行,CD=2-0=2,
S△ACD=$\frac{1}{2}$CD•(yA-yC)=$\frac{1}{2}$×2×[1-(-1)]=2.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及三角形的面积公式,解题的关键是:(1)求出点A的坐标;(2)求出点C的坐标.本题属于基础题,难度不大,解决该题型题目时,找出点的坐标,依据反比例函数图象上点的坐标特征求出反比例函数系数k是关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 射击运动员只射击1次,就命中靶心 | |
| B. | 画一个三角形,使其三边的长分别为8cm,6cm,2cm | |
| C. | 任取一个实数x,都有|x|≥0 | |
| D. | 抛掷一枚质地均匀且六个面分别刻有1到6的点数的正方体骰子,朝上一面的点数为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,1) | B. | (1,-3) | C. | (-1,-3) | D. | (-3,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
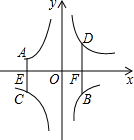 如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )
如图,A,B两点在反比例函数y=$\frac{{k}_{1}}{x}$的图象上,C、D两点在反比例函数y=$\frac{{k}_{2}}{x}$的图象上,AC⊥x轴于点E,BD⊥x轴于点F,AC=2,BD=3,EF=$\frac{10}{3}$,则k2-k1=( )| A. | 4 | B. | $\frac{14}{3}$ | C. | $\frac{16}{3}$ | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com