

分析 (1)通过解直角三角形即可得到结果;
(2)过点B作BD⊥AO交AO的延长线于D,通过解直角三角形求得BD,由C、O′、B′三点共线可得结果;
(3)显示屏O′B′应绕点O′按顺时针方向旋转30°,求得∠EO′B′=∠FO′A=30°,既是显示屏O′B′应绕点O′按顺时针方向旋转30°.
解答 解:(1)∵O′C⊥OA于C,OA=OB=24cm,O’C=12,
∴$sin∠CAO'=\frac{O'C}{O'A}=\frac{O'C}{OA}=\frac{12}{24}=\frac{1}{2}$.
∴∠CAO'=30°.
(2)如图,过点B作BD⊥AO交AO的延长线于点D.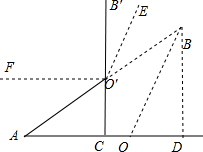
∵$sin∠BOD=\frac{BD}{OB}$,
∴BD=OB•sin∠BOD.
∵∠AOB=120°,
∴∠BOD=60°.
∴$BD=OB•sin∠BOD=24×\frac{{\sqrt{3}}}{2}=12\sqrt{3}$.
∴显示屏的顶部B'比原来升高了$({36-12\sqrt{3}})$cm.
(3)显示屏O'B'应绕点O'按顺时针方向旋转30°.
理由如下:
如图,电脑显示屏O'B’绕点O'按顺时针方向旋转α度至O'E处,O'F∥OA.
∵电脑显示屏O'B’与水平线的夹角仍保持120°,
∴∠EO'F=120°.
∴∠FO'A=∠CAO'=30°.
∴∠AO'B'=120°.
∴∠EO'B'=∠FO'A=30°,即α=30°.
∴显示屏O'B'应绕点O'按顺时针方向旋转30°.
点评 本题考查了解直角三角形的应用,旋转的性质,正确的画出图形是解题的关键.


科目:初中数学 来源: 题型:解答题
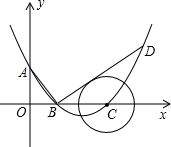 如图,在平面直角坐标系中,抛物线交y轴于A点,交x轴于B(2,0),C(6,0)两点.已知A点坐标为(0,3).
如图,在平面直角坐标系中,抛物线交y轴于A点,交x轴于B(2,0),C(6,0)两点.已知A点坐标为(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-x-1与反比例函数y=$\frac{m}{x}$的图象交于点A,一次函数y=-x-1与坐标轴分别交于B、C两点,连结AO,若tan∠AOB=$\frac{1}{2}$.
如图,一次函数y=-x-1与反比例函数y=$\frac{m}{x}$的图象交于点A,一次函数y=-x-1与坐标轴分别交于B、C两点,连结AO,若tan∠AOB=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )
如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10,则该直线的函数表达式是( )| A. | y=x+5 | B. | y=x+10 | C. | y=-x+5 | D. | y=-x+10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
如图,?ABCD中,AB=2,AD=1,∠ADC=60°,将?ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为3m.
如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为3m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com