
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点,若AE=![]() ,∠EAF=135°,则下列结论正确的是( )
,∠EAF=135°,则下列结论正确的是( )
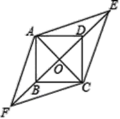
A. DE=1B. tan∠AFO=![]() C. AF=
C. AF=![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为![]()
【答案】C
【解析】
根据正方形的性质求出AO的长,用勾股定理求出EO的长,然后由∠EAF=135°及∠BAD=90°可以得到相似三角形,根据相似三角形的性质求出BF的长,再一一计算即可判断.
解:∵四边形ABCD是正方形,
∴AB=CB=CD=AD=1,AC⊥BD,∠ADO=∠ABO=45°,
∴OD=OB=OA=![]() ,∠ABF=∠ADE=135°,
,∠ABF=∠ADE=135°,
在Rt△AEO中,EO=![]() ,
,
∴DE=![]() ,故A错误.
,故A错误.
∵∠EAF=135°,∠BAD=90°,
∴∠BAF+∠DAE=45°,
∵∠ADO=∠DAE+∠AED=45°,
∴∠BAF=∠AED,
∴△ABF∽△EDA,
∴![]() ,
,
∴![]() ,
,
AF=![]() ,故C正确,
,故C正确,
OF=![]()
tan∠AFO=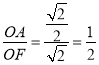 ,故B错误,
,故B错误,
∴S四边形AECF=![]() ACEF=
ACEF=![]() ×
×![]() ×
×![]() =
=![]() ,故D错误,
,故D错误,
故选:C.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
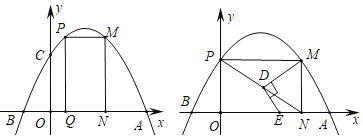
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于C点,A(5,0)且AB=3OC,P为x轴上方抛物线上的动点(P不与A,B重合),过点P作PQ⊥x轴于点Q,作PM与x轴平行,交抛物线另一点M,以PQ,PM为邻边作矩形PQNM.
(1)求抛物线的函数表达式;
(2)设矩形PQNM的周长为C,求C的取值范围;
(3)如图2,当P点与C点重合时,连接对角线PN,取PN上一点D(不与P,N重合),连接DM,作DE⊥DM,交x轴于点E.
①试求![]() 的值;
的值;
②试探求是否存在点D,使△DEN是等腰三角形?若存在,请直接写出符合条件的点D坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红乘坐小船往返于A、B两地,其中从A地到B地是顺流行驶.当小红第一次从A地出发时,小明同时乘坐橡皮艇从A、B之间的C地漂流而下,直至到达B地.已知A地分别距离B、C两地20千米和8千米,小船顺流速度为20千米/时,逆流速度为10千米/时,则小红、小明在途中相遇时距离C地_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
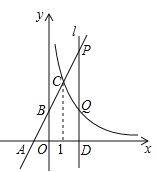
【题目】如图,一次函数y=mx+2与x轴、y轴分别交于点A(-1,0)和点B,与反比例函数![]() 的图像在第一象限内交于C(1,c).
的图像在第一象限内交于C(1,c).
(1)求m的值和反比例函数的表达式;
(2)过x轴上的点D(a,0)作平行于轴的直线![]() (a﹥1),分别与直线AB和双曲线
(a﹥1),分别与直线AB和双曲线![]() 交于点P、Q,且PQ=2QD,求点D的坐标.
交于点P、Q,且PQ=2QD,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
(1)求证:△DCE≌△BFE;
(2)若CD=2,∠ADB=30°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
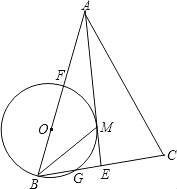
【题目】已知如图,△ABC中AB=AC,AE是角平分线,BM平分∠ABC交AE于点M,经过B、M两点的⊙O交BC于G,交AB于点F,FB恰为⊙O的直径.
(1)求证:AE与⊙O相切;
(2)当BC=6,cosC=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
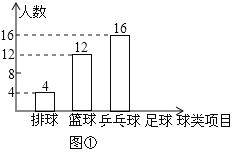

(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
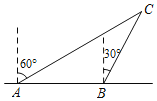
【题目】如图所示,一艘轮船在近海处由西向东航行,点C处有一灯塔,灯塔附近30海里的圆形区域内有暗礁,轮船在A处测得灯塔在北偏东60°方向上,轮船又由A向东航行40海里到B处,测得灯塔在北偏东30°方向上.
(1)求轮船在B处时到灯塔C处的距离是多少?
(2)若轮船继续向东航行,有无触礁危险?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com