
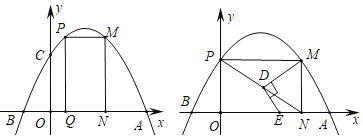
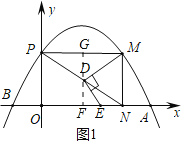
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于C点,A(5,0)且AB=3OC,P为x轴上方抛物线上的动点(P不与A,B重合),过点P作PQ⊥x轴于点Q,作PM与x轴平行,交抛物线另一点M,以PQ,PM为邻边作矩形PQNM.
(1)求抛物线的函数表达式;
(2)设矩形PQNM的周长为C,求C的取值范围;
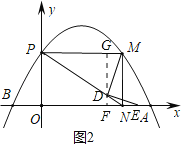
(3)如图2,当P点与C点重合时,连接对角线PN,取PN上一点D(不与P,N重合),连接DM,作DE⊥DM,交x轴于点E.
①试求![]() 的值;
的值;
②试探求是否存在点D,使△DEN是等腰三角形?若存在,请直接写出符合条件的点D坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+
x2+![]() x+2;(2)C的取值范围是0≤C≤
x+2;(2)C的取值范围是0≤C≤![]() ;(3)①2,②存在点D,使△DEN是等腰三角形,符合条件的点D坐标为(
;(3)①2,②存在点D,使△DEN是等腰三角形,符合条件的点D坐标为(![]() ,
,![]() )与(
)与(![]() ,2﹣
,2﹣![]() ).
).
【解析】
(1)先求出点C坐标,由AB=3OC和点A坐标得到点B坐标,用待定系数法即求出抛物线解析式.
(2)设点P坐标(p,![]() ),即能用p表示PQ;由PM∥x轴可知P、M关于抛物线对称轴对称,即P、M到对称轴的距离相等,故能用p表示M的横坐标,进而表示PM的长;由矩形PQNM周长等于PQ与PM的和的2倍,即用含p的二次式表示周长C,配方即得到其最值.再根据p的取值范围,即能求C的取值范围.
),即能用p表示PQ;由PM∥x轴可知P、M关于抛物线对称轴对称,即P、M到对称轴的距离相等,故能用p表示M的横坐标,进而表示PM的长;由矩形PQNM周长等于PQ与PM的和的2倍,即用含p的二次式表示周长C,配方即得到其最值.再根据p的取值范围,即能求C的取值范围.
(3)①由P点与C点重合即求得P、M、N的坐标;由DE⊥DM,过D作x轴垂线FG,即构造出△MDG∽△DEF,所以![]() .
.
②对点E在点N左侧和右侧进行分类讨论:若点E在点N左侧,先说明∠DEN为钝角,所以△DEN为等腰三角形时只有DE=EN一种情况.设点D横坐标为d,求直线PN解析式即得到D的纵坐标,进而能用d表示所有线段的长,再在Rt△DEF中利用勾股定理列方程,即求出d的值;若点E在点N右侧,说明∠DNE为钝角,得DN=EN,解题思路与第一种情况相同,即求出d的值.
(1)当x=0时,y=ax2+bx+2=2
∴C(0,2),OC=2
∴AB=3OC=6
∵A(5,0),即OA=5
∴OB=AB﹣OA=1
∴B(﹣1,0)
把A、B坐标代入抛物线解析式得:
![]() 解得:
解得: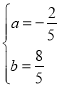
∴抛物线的函数表达式为![]()
(2)设P(p, ![]() )
)
∵PQ⊥x轴于Q,PM∥x轴
∴PQ=![]() ,点P、M关于抛物线对称轴对称
,点P、M关于抛物线对称轴对称
∵抛物线对称轴:直线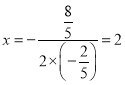
∴xM=2+(2﹣p)=4﹣p
∴PM=(4﹣p)﹣p=4﹣2p
∴C=2(PM+PQ)=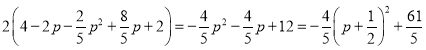
∵﹣1<p<5
∴当p=![]() 时,C有最大值为
时,C有最大值为![]()
∴C的取值范围是0≤C≤![]()
(3)①过点D作GF⊥x轴于点F,交PM于G
∴∠DFE=∠DGM=90°,DF∥y轴
∴四边形MNFG是矩形,△DFN∽△PON
∴![]()
∵P点与C点重合,P、M关于直线x=2对
∴P(0,2),M(4,2),N(4,0)
∴GF=MN=OP=2,PM=ON=4
∴![]()
∵DE⊥DM
∴∠MDE=90°
∴∠MDG+∠EDF=∠EDF+∠DEF=90°
∴∠MDG=∠DEF
∴△MDG∽△DEF
∴![]()
②存在点D,使△DEN是等腰三角形
设直线PN解析式为y=mx+n
∴ ![]() 解得:
解得: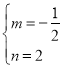
∴直线PN解析式为y=﹣![]() x+2
x+2
设D(d,﹣![]() d+2)(0<d<4)
d+2)(0<d<4)
∴OF=d,DF=﹣![]() d+2
d+2
∴FN=ON﹣OF=4﹣d,DG=FG﹣DF=2﹣(﹣![]() d+2)=
d+2)=![]() d
d
∵△MDG∽△DEF
∴![]()
∴EF=![]() DG=
DG=![]() d
d
①当点E在点N左侧时,如图1,
∵四边形DENM中,∠MDE=∠MNE=90°,∠DMN<90°
∴∠DEN=360°﹣∠MDE﹣∠MNE﹣∠DMN=180°﹣∠DMN>90°
∴当△DEN是等腰三角形时,DE=EN=FN﹣EF=![]() ,
,
∵Rt△DEF中,DF2+EF2=DE2
∴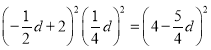
解得:d1=4(舍去),![]() ,
,
∴![]()
∴点D坐标为![]()
②当点E在点N右侧时,如图2,∠DNE>90°
∴当△DEN是等腰三角形时,DN=EN=EF﹣FN=![]() ,
,
∵Rt△DFN中,DF2+FN2=DN2
∴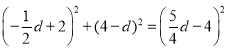
解得:![]() ,
,![]() (舍去)
(舍去)
∴![]()
∴点D坐标为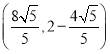
综上所述,符合条件的点D坐标为![]() 与
与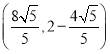 .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣4,1),B(﹣1,3),C(﹣1,1)
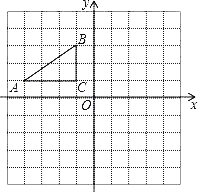
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;平移△ABC,若A对应的点A2坐标为(﹣4,﹣5),画出△A2B2C2;
(2)若△A1B1C1绕某一点旋转可以得到△A2B2C2,直接写出旋转中心坐标 .
(3)在x轴上有一点P使得PA+PB的值最小,直接写出点P的坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
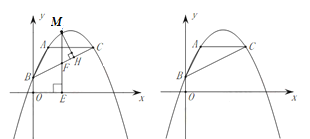
【题目】如图,在平面直角坐标系中,抛物线![]() ,经过点
,经过点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴的平行线交抛物线于另一点
轴的平行线交抛物线于另一点![]() .
.
(1)求抛物线的表达式及其顶点坐标;
(2)如图,点![]() 是第一象限中
是第一象限中![]() 上方抛物线上的一个动点,过点作
上方抛物线上的一个动点,过点作![]() 于点
于点![]() ,作
,作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,在点
,在点![]() 运动的过程中,
运动的过程中,![]() 的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
的周长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图,连接![]() ,在
,在![]() 轴上取一点
轴上取一点![]() ,使
,使![]() 和
和![]() 相似,请求出符合要求的点
相似,请求出符合要求的点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高5米的小区超市,超市以上是居民住房.在该楼的前面15米处要盖一栋高20米的新楼.当冬季正午的阳光与水平线的夹角为32°时.
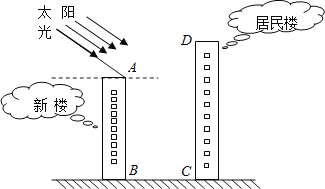
(1)问超市以上的居民住房采光是否有影响,为什么?
(2)若要使超市采光不受影响,两楼应相距多少米?(结果保留整数,参考数据:sin32°≈![]() ,cos32°≈
,cos32°≈![]() ,tan32°≈
,tan32°≈![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为400平方米的花坛区域进行绿化,安排甲工程队或乙工程队完成.已知甲队平均每天完成绿化的面积是乙队的2倍,并且甲队比乙队能少用4天完成任务,求甲、乙两工程队平均每天能完成绿化的面积分别是多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营A种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量.
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付仓库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】特产店销售一种水果,其进价每千克40元,按60元出售,平均每天可售100千克,后来经过市场调查发现,单价每降低2元,则平均每天可增加20千克销量.
(1)若该专卖店销售这种核桃要想平均每天获利2240元,每千克水果应降多少元?
(2)若该专卖店销售这种核桃要想平均每天获利最大,每千克水果应降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
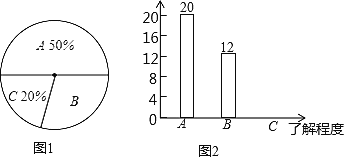
【题目】双峰县教育局要求各学校加强对学生的安全教育,全县各中小学校引起高度重视,小刚就本班同学对安全知识的了解程度进行了一次调查统计.他将统计结果分为三类,A:熟悉;B:了解较多;C:一般了解。图①和图②是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求小刚所在的班级共有多少名学生;
(2)在条形图中,将表示“一般了解”的部分补充完整‘’
(3)在扇形统计图中,计算“了解较多”部分所对应的扇形圆心角的度数;
(4)如果小刚所在年级共1000名同学,请你估算全年级对安全知识“了解较多”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
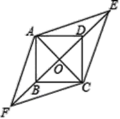
【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点,若AE=![]() ,∠EAF=135°,则下列结论正确的是( )
,∠EAF=135°,则下列结论正确的是( )
A. DE=1B. tan∠AFO=![]() C. AF=
C. AF=![]() D. 四边形AFCE的面积为
D. 四边形AFCE的面积为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com