
【题目】特产店销售一种水果,其进价每千克40元,按60元出售,平均每天可售100千克,后来经过市场调查发现,单价每降低2元,则平均每天可增加20千克销量.
(1)若该专卖店销售这种核桃要想平均每天获利2240元,每千克水果应降多少元?
(2)若该专卖店销售这种核桃要想平均每天获利最大,每千克水果应降多少元?
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.

(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级共有6个班,要从中选出两个班代表学校参加一项重大活动,九(1)班是先进班,学校指定该班必须参加,另外再从九(2)班到九(6)班中选出一个班,九(4)班有同学建议用如下方法选班:从装有编号为1,2,3的三个白球的A袋中摸出一个球,再从装有编号也为1,2,3的三个红球的B袋中摸出一个球(两袋中球的大小、形状与质地完全一样),摸出的两个球编号之和是几就派几班参加.
(1)请用列表或画树形图的方法列举出摸出的两球编号的所有可能出现的结果;
(2)如果采用这一建议选班,对五个班是一样公平的吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
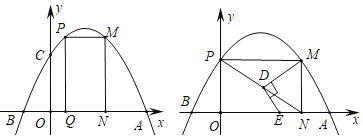
【题目】如图1,抛物线y=ax2+bx+2与x轴交于A,B两点,与y轴交于C点,A(5,0)且AB=3OC,P为x轴上方抛物线上的动点(P不与A,B重合),过点P作PQ⊥x轴于点Q,作PM与x轴平行,交抛物线另一点M,以PQ,PM为邻边作矩形PQNM.
(1)求抛物线的函数表达式;
(2)设矩形PQNM的周长为C,求C的取值范围;
(3)如图2,当P点与C点重合时,连接对角线PN,取PN上一点D(不与P,N重合),连接DM,作DE⊥DM,交x轴于点E.
①试求![]() 的值;
的值;
②试探求是否存在点D,使△DEN是等腰三角形?若存在,请直接写出符合条件的点D坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
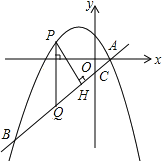
【题目】如图,在平面直角坐标系中,直线y=![]() 与抛物线y=
与抛物线y=![]() 交于A、B两点,且点A在x轴上,点B的横坐标为-4,点P为直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点Q,PH⊥AB于H.
交于A、B两点,且点A在x轴上,点B的横坐标为-4,点P为直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点Q,PH⊥AB于H.
(1)求b的值及sin∠PQH的值;
(2)设点P的横坐标为t,用含t的代数式表示点P到直线AB的距离PH的长,并求出PH之长的最大值以及此时t的值;
(3)连接PB,若线段PQ把△PBH分成成△PQB与△PQH的面积相等,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是我国古代数学的经典著作,书中有一个问题:“今有黄金九枚,白银一十一枚,称之重适等.交易其一,金轻十三两.问金、银一枚各重几何?”.意思是:甲袋中装有黄金9枚(每枚黄金重量相同),乙袋中装有白银11枚(每枚白银重量相同),称重两袋相等.两袋互相交换1枚后,甲袋比乙袋轻了13两(袋子重量忽略不计).问黄金、白银每枚各重多少两?设每枚黄金重x两,每枚白银重y两,根据题意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB,∠CAB的平分线AE交CD于点H、交CB于点E,EF⊥AB于点F,则下列结论中不正确的是( )
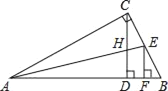
A. ∠ACD=∠BB. CH=CE=EFC. CH=HDD. AC=AF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红乘坐小船往返于A、B两地,其中从A地到B地是顺流行驶.当小红第一次从A地出发时,小明同时乘坐橡皮艇从A、B之间的C地漂流而下,直至到达B地.已知A地分别距离B、C两地20千米和8千米,小船顺流速度为20千米/时,逆流速度为10千米/时,则小红、小明在途中相遇时距离C地_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
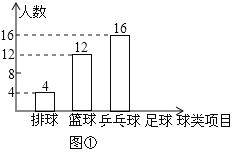

(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com