练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】某校为美化校园，计划对面积为400平方米的花坛区域进行绿化，安排甲工程队或乙工程队完成．已知甲队平均每天完成绿化的面积是乙队的2倍，并且甲队比乙队能少用4天完成任务，求甲、乙两工程队平均每天能完成绿化的面积分别是多少平方米？

    【答案】甲工程队平均每天能完成绿化的面积是100平方米，乙工程队平均每天能完成绿化的面积是50平方米．

    【解析】

    设乙工程队平均每天能完成绿化的面积是x平方米，则甲工程队平均每天能完成绿化的面积是2x平方米，根据工作时间＝工作总量÷工作效率结合甲队比乙队能少用4天完成任务，即可得出关于x的分式方程，解之经检验后即可得出结论．

    设乙工程队平均每天能完成绿化的面积是x平方米，则甲工程队平均每天能完成绿化的面积是2x平方米，

    依题意，得: ，

    解得：x＝50，

    经检验，x＝50是原方程的解，且符合题意，

    ∴2x＝100．

    答：甲工程队平均每天能完成绿化的面积是100平方米，乙工程队平均每天能完成绿化的面积是50平方米．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

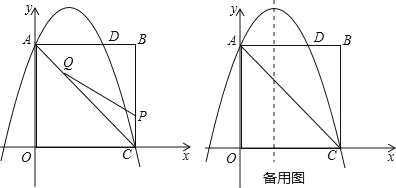
    【题目】如图，在矩形OABC中，点O为原点，点A的坐标为(0，8)，点C的坐标为(6，0)．抛物线y＝﹣x2+bx+c经过点A、C，与AB交于点D．

    (1)求抛物线的函数解析式；

    (2)点P为线段BC上一个动点(不与点C重合)，点Q为线段AC上一个动点，AQ＝CP，连接PQ，设CP＝m，△CPQ的面积为S．

    ①求S关于m的函数表达式；

    ②当S最大时，在抛物线y＝﹣x2+bx+c的对称轴l上，若存在点F，使△DFQ为直角三角形，请直接写出所有符合条件的点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

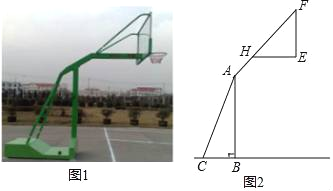
    【题目】如图1，2分别是某款篮球架的实物图与示意图，已知AB⊥BC于点B，底座BC的长为1米，底座BC与支架AC所成的角∠ACB＝60°，点H在支架AF上，篮板底部支架EH∥BC，EF⊥EH于点E，已知AH长米，HF长米，HE长1米．

    (1)求篮板底部支架HE与支架AF所成的角∠FHE的度数．

    (2)求篮板底部点E到地面的距离．(结果保留根号)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某中学九年级共有6个班，要从中选出两个班代表学校参加一项重大活动，九（1）班是先进班，学校指定该班必须参加，另外再从九（2）班到九（6）班中选出一个班，九（4）班有同学建议用如下方法选班：从装有编号为1，2，3的三个白球的A袋中摸出一个球，再从装有编号也为1，2，3的三个红球的B袋中摸出一个球（两袋中球的大小、形状与质地完全一样），摸出的两个球编号之和是几就派几班参加．

    （1）请用列表或画树形图的方法列举出摸出的两球编号的所有可能出现的结果；

    （2）如果采用这一建议选班，对五个班是一样公平的吗？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，AB＝BC＝5，AC＝6．△ECD是△ABC沿BC方向平移得到的，连接AE．AC和BE相交于点O．

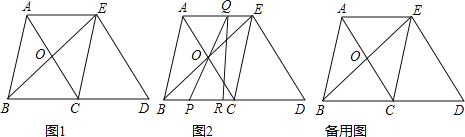
    （1）判断四边形ABCE是怎样的四边形，说明理由；

    （2）如图2，P是线段BC上一动点（图2），（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R．

    ①四边形PQED的面积是否随点P的运动而发生变化．若变化，请说明理由；若不变，求出四边形PQED的面积；

    ②当线段PB的长为何值时，△PQR与△BOC相似．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

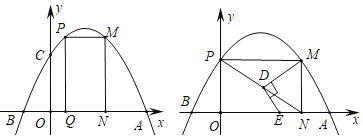
    【题目】如图1，抛物线y＝ax2+bx+2与x轴交于A，B两点，与y轴交于C点，A（5，0）且AB＝3OC，P为x轴上方抛物线上的动点（P不与A，B重合），过点P作PQ⊥x轴于点Q，作PM与x轴平行，交抛物线另一点M，以PQ，PM为邻边作矩形PQNM．

    （1）求抛物线的函数表达式；

    （2）设矩形PQNM的周长为C，求C的取值范围；

    （3）如图2，当P点与C点重合时，连接对角线PN，取PN上一点D（不与P，N重合），连接DM，作DE⊥DM，交x轴于点E．

    ①试求的值；

    ②试探求是否存在点D，使△DEN是等腰三角形？若存在，请直接写出符合条件的点D坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

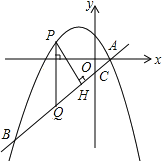
    【题目】如图，在平面直角坐标系中，直线y=与抛物线y=交于A、B两点，且点A在x轴上，点B的横坐标为-4，点P为直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线交直线AB于点Q，PH⊥AB于H．

    （1）求b的值及sin∠PQH的值；

    （2）设点P的横坐标为t，用含t的代数式表示点P到直线AB的距离PH的长，并求出PH之长的最大值以及此时t的值；

    （3）连接PB，若线段PQ把△PBH分成成△PQB与△PQH的面积相等，求此时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠ACB＝90°，CD⊥AB，∠CAB的平分线AE交CD于点H、交CB于点E，EF⊥AB于点F，则下列结论中不正确的是（　　）

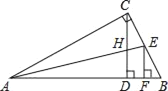
    A. ∠ACD＝∠BB. CH＝CE＝EFC. CH＝HDD. AC＝AF

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将矩形纸片ABCD沿对角线BD折叠，使点A落在平面上的F点处，DF交BC于点E．

    （1）求证：△DCE≌△BFE；

    （2）若CD=2，∠ADB=30°，求BE的长．

    查看答案和解析>>

    同步练习册答案