
【题目】如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
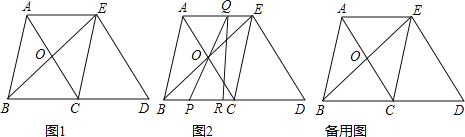
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化.若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段PB的长为何值时,△PQR与△BOC相似.
【答案】(1)菱形,证明见解析;(2)①不变,24;②PB=![]() .
.
【解析】
解:(1)四边形ABCE是菱形.
∵△ECD是由△ABC沿BC平移得到的,
∴EC∥AB,且EC=AB,
∴四边形ABCE是平行四边形,
又∵AB=BC,
∴四边形ABCE是菱形;
(2)①四边形PQED的面积不发生变化.
方法一:∵ABCE是菱形,
∴AC⊥BE,OC=![]() AC=3,
AC=3,
∵BC=5,
∴BO=4,
过A作AH⊥BD于H,(如图1)

∵![]() ,
,
即![]() ,
,
解得AH=![]() .
.
或∵∠AHC=∠BOC=90°,∠BCA=∠BCA,
∴△AHC∽△BOC,
∴AH:BO=AC:BC,
即AH:4=6:5,
∴AH=![]() .
.
由菱形的对称性知,△PBO≌△QEO,
∴BP=QE,
∴![]()
方法二:由菱形的对称性知,△PBO≌△QEO,
∴![]() ,
,
∵△ECD是由△ABC平移得到的,
∴ED∥AC,ED=AC=6,
又∵BE⊥AC,
∴BE⊥ED,
∴![]()
![]()
![]()
![]()
![]()
=24
②方法一:如图2,

当点P在BC上运动,使△PQR与△COB相似时,
∵∠2是△OBP的外角,
∴∠2>∠3,
∴∠2不与∠3对应,
∴∠2与∠1对应,
即∠2=∠1,
∴OP=OC=3
过O作OG⊥BC于G,则G为PC的中点,
∴△OGC∽△BOC,
∴CG:CO=CO:BC,
即CG:3=3:5,
∴CG=![]() ,
,
∴![]() .
.
方法二:如图3,

当点P在BC上运动,使△PQR与△COB相似时,
∵∠2是△OBP的外角,
∴∠2>∠3,
∴∠2不与∠3对应,
∴∠2与∠1对应,
∴QR:BO=PR:OC
即![]() :4=PR:3,
:4=PR:3,
∴PR=![]() ,
,
过E作EF⊥BD于F,设PB=x,则RF=QE=PB=x,
DF=![]() ,
,
∴BD=PB+PR+RF+DF=![]() ,
,
解得x=![]() .
.
方法三:如图4,
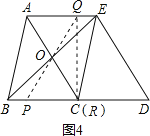
若点P在BC上运动,使点R与C重合,
由菱形的对称性知,O为PQ的中点,
∴CO是Rt△PCQ斜边上的中线,
∴CO=PO,
∴∠OPC=∠OCP,
此时,Rt△PQR∽Rt△CBO,
∴PR:CO=PQ:BC,
即PR:3=6:5,
∴PR=![]()
∴PB=BC﹣PR=![]() .
.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】有一项工程,乙队单独完成所需的时间是甲队单独完成所需时间的2倍,若两队合作4天后,剩下的工作甲单独做还需要6天完成.
(1)求甲、乙两队单独完成这项工程各需多少天;
(2)若甲队每天的报酬是1万元,乙队每天的报酬是0.3万元,要使完成这项工程时的总报酬不超过9.6万元,甲队最多可以工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
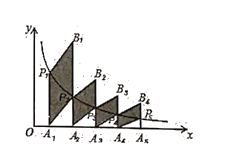
【题目】如图,分别过反比例函数![]() 图象上的点
图象上的点![]() , ...
, ...![]() ···作
···作![]() 轴的垂线,垂足分别为
轴的垂线,垂足分别为![]() ······
······![]() ,连接
,连接![]() ···
···![]() 再以
再以![]() 为一组邻边画一个平行四边形
为一组邻边画一个平行四边形![]() ,以
,以![]() 为一组邻边画一个平行四边形
为一组邻边画一个平行四边形![]()
![]() ,依此类推,则点
,依此类推,则点![]() 的纵坐标是_____.(结果用含
的纵坐标是_____.(结果用含![]() 代数式表示)
代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
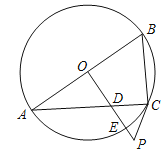
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(1)班学生即将所穿校服型号情况进行摸底调查,并根据调查结果绘制如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
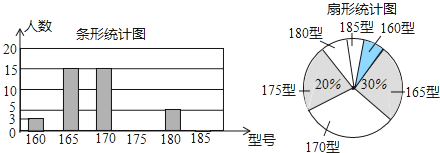
根据以上信息,解答下列问题:
(1)该班共有多少名学生?
(2)在条形统计图中,请把空缺部分补充完整;在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(3)求该班学生所穿校服型号的众数和中位数.如果该高中学校准备招收2000名高一新生,则估计需要准备多少套180型号的校服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一副直角三角板如图放置,其中BC=6,EF=8,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为_____.
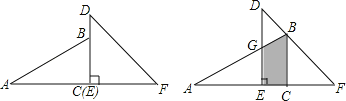
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,垂足为
,垂足为![]() ,且交
,且交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() .有如下结论:①
.有如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
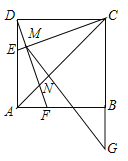
A. ①②B. ①③C. ①②③D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com