
����Ŀ��ij����ѧУΪʹ��һ������У��ʱ���Ϻ�����У��������ǰ��ijУ���꼶��1����ѧ����������У���ͺ�������������飬�����ݵ�����������ͼ������������ͳ��ͼ��У���ͺ���������Ϊ��������Ϊ6���ͺţ���
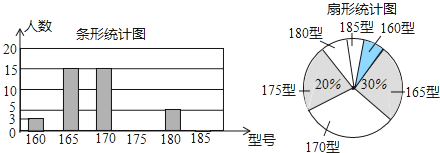
����������Ϣ������������⣺
��1���ð�ж�����ѧ����
��2��������ͳ��ͼ�У���ѿ�ȱ���ֲ���������������ͳ��ͼ�У������185��У������Ӧ������Բ�ĽǵĴ�С��
��3����ð�ѧ������У���ͺŵ���������λ��������ø���ѧУ������2000����һ�������������Ҫ��������180�ͺŵ�У����
���𰸡���1������50��ѧ������2���𰸼�������14.4������3��������165��170����λ����170��200�ף�
��������
��1������������=165�͵���������Ӧ�İٷֱ���⼴�ɣ�
��2�������175��185�͵�ѧ���������ٲ�ȫͳ��ͼ���ɣ�
��3��������������λ���Ķ��弰2000��180�ͺ���ռ�İٷֱ���⼴�ɣ�
�⣺��1��15��30%=50��������50��20%=10��������
�𣺸ð��50��ѧ�������д�175��У����ѧ����10����
��2����175��У����ѧ����10����50��20%��10��������
185�͵�ѧ������Ϊ��50-3-15-15-10-5=50-48=2��������
��ȫͳ��ͼ��ͼ��ʾ��
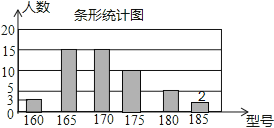
185��У������Ӧ������Բ�Ľ�Ϊ��![]() ��360����14.4����
��360����14.4����
��3��165�ͣ�170��ѧ����࣬��Ϊ15��
��ð�ѧ������У���ͺŵ�����Ϊ165��170��
���ͺŴ�С�������к�25���͵�26��ͬѧ��Ϊ170��
����λ��Ϊ170��
2000![]() ���ף�
���ף�
����Ҫ��200��180�ͺŵ�У����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
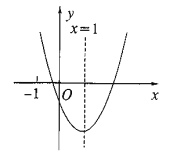
����Ŀ�����κ���![]() ��ͼ����ͼ��ʾ���Գ���Ϊ
��ͼ����ͼ��ʾ���Գ���Ϊ![]() ���������½��ۣ���
���������½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() �����У���ȷ�Ľ����У� ��
�����У���ȷ�Ľ����У� ��
A.![]() ��B.
��B.![]() ��C.
��C.![]() ��D.
��D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
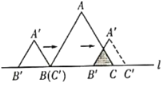
����Ŀ����ͼ���߳�Ϊ![]() �ĵȱ�
�ĵȱ�![]() �ͱ߳�Ϊ
�ͱ߳�Ϊ![]() �ĵȱ�
�ĵȱ�![]() �����ǵı�
�����ǵı�![]() ��
��![]() λ��ͬһ��ֱ��
λ��ͬһ��ֱ��![]() �ϣ���ʼʱ����
�ϣ���ʼʱ����![]() ���
���![]() �غϣ�
�غϣ�![]() �̶�������Ȼ���
�̶�������Ȼ���![]() ����������ֱ��
����������ֱ��![]() ƽ�ƣ��Ƴ�
ƽ�ƣ��Ƴ�![]() �⣨��
�⣨��![]() ���
���![]() �غϣ�ֹͣ����
�غϣ�ֹͣ����![]() ƽ�Ƶľ���Ϊ
ƽ�Ƶľ���Ϊ![]() �������������غϲ��ֵ����Ϊ
�������������غϲ��ֵ����Ϊ![]() ����
����![]() ����
����![]() �ĺ���ͼ���ǣ� ��
�ĺ���ͼ���ǣ� ��
A.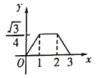 B.
B.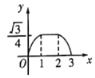 C.
C.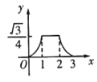 D.
D.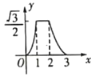
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڡ�ABC�У�AB��BC��5��AC��6����ECD�ǡ�ABC��BC����ƽ�Ƶõ��ģ�����AE��AC��BE�ཻ�ڵ�O��
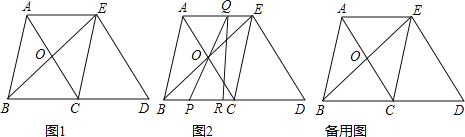
��1���ж��ı���ABCE���������ı��Σ�˵�����ɣ�
��2����ͼ2��P���߶�BC��һ���㣨ͼ2�����������B��C�غϣ�������PO���ӳ����߶�AE�ڵ�Q��QR��BD������Ϊ��R��
���ı���PQED������Ƿ����P���˶��������仯�����仯����˵�����ɣ������䣬����ı���PQED�������
�ڵ��߶�PB�ij�Ϊ��ֵʱ����PQR���BOC���ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�����P�ӵ�B��������BC��CD��DA�˶�����Aֹͣ�����P�˶���·��Ϊx����ABP�����Ϊy����y����x�ĺ���ͼ����ͼ2��ʾ����y�����ֵ�ǣ�������
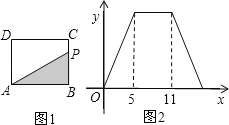
A.55B.30C.16D.15
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
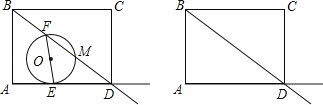
����Ŀ����ͼ������ABCD�У�AB��6��AD��8������E��Fͬʱ�ֱ�ӵ�A��B�������ֱ���������AD������BD�ķ������ÿ��1����λ���ٶ��˶�������EF����EFΪֱ������O������BD�ڵ�M�����˶���ʱ��Ϊt��
��1������E���߶�AD��ʱ���ù���t�Ĵ���ʽ��ʾDE��DM��
��2���������˶������У�
������CM����tΪ��ֵʱ����CDMΪ���������Σ�
��Բ��O���ھ���ABCD�ڣ������߽磩ʱ����t��ȡֵ��Χ����ֱ��д���ڴ˷�Χ��Բ���˶���·������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ����ѧ����Ұ����չ����������ܡ�����������������˾��꼶����ѧ��һ�ܵĿ����Ķ�ʱ�䣬����������Ƴ�������������ͳ��ͼ���������ͳ��ͼ��ͼ1������Ϣ�ش��������⣺
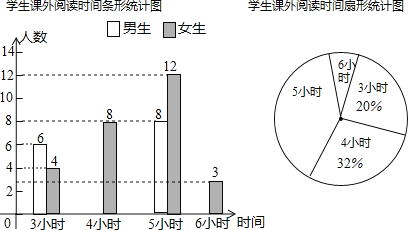
��1�����ε����ѧ������Ϊ________�ˣ�������ѧ���Ŀ����Ķ�ʱ�����λ����________Сʱ��������_________Сʱ��
��2�����㲹ȫ����ͳ��ͼ��������ͳ��ͼ�У������Ķ�ʱ��Ϊ![]() Сʱ�����ε�Բ�ĽǶ�����_________��
Сʱ�����ε�Բ�ĽǶ�����_________��
��3����ȫУ���꼶����ѧ��![]() �ˣ����ƾ��꼶һ�ܿ����Ķ�ʱ��Ϊ
�ˣ����ƾ��꼶һ�ܿ����Ķ�ʱ��Ϊ![]() Сʱ��ѧ���ж����ˣ�
Сʱ��ѧ���ж����ˣ�
��4����ѧУѡȡ![]() ��
��![]() ��
��![]() ��
��![]() ���˲μ��Ķ�����������һ���Ϊ���飬��
���˲μ��Ķ�����������һ���Ϊ���飬��![]() ��
��![]() ��һ��ĸ��ʣ����б�����״ͼ��
��һ��ĸ��ʣ����б�����״ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ԡ�ABC�ı�ABΪֱ���ġ�O���AC�ཻ�ڵ�D��BC�ǡ�O�����ߣ�EΪBC���е㣬����BD��DE��
��1����DE�ǡ�O�����ߣ�
��2�����CDE�����ΪS1���ı���ABED�����ΪS2����S2��5S1����tan��BAC��ֵ��
��3���ڣ�2���������£�����AE������O�İ뾶Ϊ2����AE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����������һ���Ƕȵķ���������ڲ����ǿ��������������£�С��ķ��и߶�y(m)�����ķ���ʱ��x(s)������κ�����ϵ��y��x�ļ����Ӧֵ���±���ʾ��
x(s) | 0 | 0.5 | 1 | 1.5 | 2 | �� |
y(m) | 0 | 8.75 | 15 | 18.75 | 20 | �� |
(��)��y����x�ĺ�������ʽ(��Ҫ��дx��ȡֵ��Χ)��
(��)�ʣ�С��ķ��и߶��ܷ�ﵽ22m����˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com