
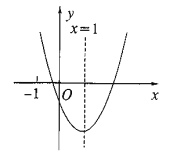
【题目】二次函数![]() 的图象如图所示,对称轴为
的图象如图所示,对称轴为![]() .给出以下结论:①
.给出以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中,正确的结论有( )
.其中,正确的结论有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
【答案】B
【解析】
根据二次函数的图象的开口方向,对称轴以及与y轴的交点位置可判断出a,b,c的取值范围,从而可对①判断;根据抛物线与x轴的交点个数对②进行判断;根据抛物线的对称性确定x=2时y的取值即可对③进行判断;由对称轴x=1可求出b=2a,再根据x=-1结合函数的图象确定y的取值范围即可对④进行判断,从而可求出本题的答案.
①∵函数图象开口向上,
∴a>0,
∵函数图象与y轴的负半轴相交,
∴c<0,
∵抛物线的对称轴在y轴的右侧,
∴![]() ,
,
∴b>0,
∴abc<0,故①错误;
②∵函数图象与x轴有两个交点,
∴△=b2-4ac>0,
∴![]() ,故②正确;
,故②正确;
③抛物线上的点(0,y)关于直线x=1对称点的坐标为(2,y),
∵x=0时,y=c<0,
∴x=2时,y=4a+2b+c<0,故③错误;
④由对称轴可知:![]() ,
,
∴b=-2a,
∴当x=-1时,
y=a-b+c>0,
即3a+c>0,故④正确;
故选:B.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张正面标有数字![]() ,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
(1)第一次抽到数字2的卡片的概率是 ;
(2)设第一次抽到的数字为![]() ,第二次抽到的数字为
,第二次抽到的数字为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,请用树状图或列表法求点
,请用树状图或列表法求点![]() 在第三象限的概率.
在第三象限的概率.
![]()
![]()
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家销售一种产品,现准备从网上销售和市场直销两种销售方案中选择一种进行销售.由于受各种不确定因素影响,不同销售的方案会产生不同的成本和其它费用.设每月销售x件,网上销售月利润为w网(元),市场直销月利润为w市(元),具体信息如表:
每件售价(元) | 每件成本(元) | 月其他费用(元) | |
网上销售 | - | 20 | 45000 |
市场直销 | 120 | k |
|
其中k为常数,且30≤k≤50.月利润=月销售额-月成本-月其它费用.
(1)当x=500时,网上销售单价为______元.
(2)分别求出w网,w市与x间的函数解析式(不必写x的取值范围).
(3)若网上销售月利润的最大值与市场直销月利润的最大值相同,求k的值.
(4)如果某月要将3000件产品全部销售完,请你通过分析帮厂家做出决策,选择在网上销售还是市场直销才能使月利润较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用下面的折线统计图表示:(甲为实线,乙为虚线)
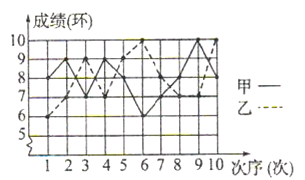
(1)依据折线统计图,得到下面的表格:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 |
| 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 |
| 10 |
其中![]() ________,
________,![]() ________;
________;
(2)甲成绩的众数是________环,乙成绩的中位数是________环;
(3)请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?
(4)该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
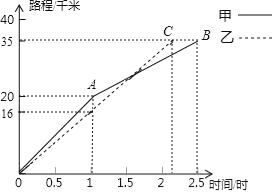
【题目】2018年,广州国际龙舟邀请赛于6月23日在中山大学北门广场至广州大桥之间的珠江河段举行.上午8时,参赛龙舟同时出发,甲、乙两队在比赛中,路程y(千米)与时间x(小时)的函数关系如图所示,甲队在上午11时30分到达终点.
(1)在比赛过程中,乙队何时追上甲队?
(2)在比赛过程中,甲、乙两队何时相距最远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一项工程,乙队单独完成所需的时间是甲队单独完成所需时间的2倍,若两队合作4天后,剩下的工作甲单独做还需要6天完成.
(1)求甲、乙两队单独完成这项工程各需多少天;
(2)若甲队每天的报酬是1万元,乙队每天的报酬是0.3万元,要使完成这项工程时的总报酬不超过9.6万元,甲队最多可以工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(1)班学生即将所穿校服型号情况进行摸底调查,并根据调查结果绘制如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
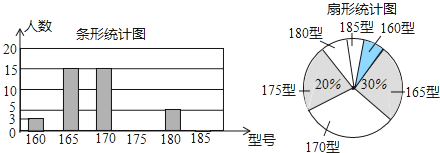
根据以上信息,解答下列问题:
(1)该班共有多少名学生?
(2)在条形统计图中,请把空缺部分补充完整;在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(3)求该班学生所穿校服型号的众数和中位数.如果该高中学校准备招收2000名高一新生,则估计需要准备多少套180型号的校服?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com