
【题目】如图,有四张正面标有数字![]() ,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
(1)第一次抽到数字2的卡片的概率是 ;
(2)设第一次抽到的数字为![]() ,第二次抽到的数字为
,第二次抽到的数字为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,请用树状图或列表法求点
,请用树状图或列表法求点![]() 在第三象限的概率.
在第三象限的概率.
![]()
![]()
![]()
![]()
科目:初中数学 来源: 题型:
【题目】(1)数轴上有A、B两点,若A点对应的数是﹣2,且A、B两点间的距离为3,则点B对应的数是________;
(2)已知线段AB=12cm,直线AB上有一点C,且BC=4cm,M是AC的中点,AM的长为________;
(3)已知∠AOB=3∠BOC,∠BOC=30°,则∠AOC=________;
(4)已知等腰三角形两边长为17、8,求三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
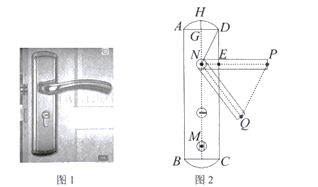
【题目】小明家的门框上装有一把防盗门锁(如图1)其平面结构图如图2所示,锁身可以看成由两条等弧![]() 和矩形
和矩形![]() 组成,
组成,![]() 的圆心是倒锁按钮点
的圆心是倒锁按钮点![]() .其中
.其中![]() 的弓高
的弓高![]()
![]() .当锁柄
.当锁柄![]() 绕着点
绕着点![]() 旋转至
旋转至![]() 位置时,门锁打开,此时直线
位置时,门锁打开,此时直线![]() 与
与![]() 所在圆相切,且
所在圆相切,且![]() 则
则![]() 的长度约为____________
的长度约为____________![]() .(结果精确到
.(结果精确到![]() ,参考数据:
,参考数据:![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一个三角形一条边上的高等于这条边长的一半,则称该三角形为“半高”三角形,这条高称为“半高”.

(1)如图1,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 求证:
求证: ![]() 是“半高”三角形;
是“半高”三角形;
(2)如图2,![]() 是“半高”三角形,且
是“半高”三角形,且![]() 边上的高是“半高”,点
边上的高是“半高”,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
①请探究![]() ,
,![]() ,
,![]() 之间的等量关系,并说明理由;
之间的等量关系,并说明理由;
②若![]() 的面积等于16,求
的面积等于16,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
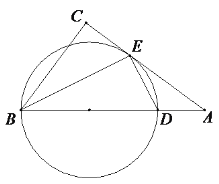
【题目】如图,Rt△ABC中,∠C=90°,∠B的平分线交AC于E,DE⊥BE.
(1)试说明AC是△BED外接圆的切线;
(2)若CE=1,BC=2,求△ABC内切圆的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
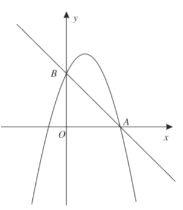
【题目】已知一次函数![]() 与二次函数
与二次函数![]() 的图象的一个交点坐标为
的图象的一个交点坐标为![]() ,另一个交点
,另一个交点![]() 在
在![]() 轴上,点
轴上,点![]() 为
为![]() 轴右侧抛物线上的一动点.
轴右侧抛物线上的一动点.
(1)求此二次函数的解析式;
(2)当点![]() 位于直线
位于直线![]() 上方的抛物线上时,求
上方的抛物线上时,求![]() 面积的最大值;
面积的最大值;
(3)当此抛物线在点![]() 与点
与点![]() 之间的部分(含点
之间的部分(含点![]() 和点
和点![]() )的最高点与最低点的纵坐标之差为9时,请直接写出点
)的最高点与最低点的纵坐标之差为9时,请直接写出点![]() 的坐标和
的坐标和![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
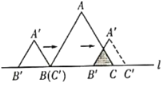
【题目】如图,边长为![]() 的等边
的等边![]() 和边长为
和边长为![]() 的等边
的等边![]() ,它们的边
,它们的边![]() ,
,![]() 位于同一条直线
位于同一条直线![]() 上,开始时,点
上,开始时,点![]() 与点
与点![]() 重合,
重合,![]() 固定不动,然后把
固定不动,然后把![]() 自左向右沿直线
自左向右沿直线![]() 平移,移出
平移,移出![]() 外(点
外(点![]() 与点
与点![]() 重合)停止,设
重合)停止,设![]() 平移的距离为
平移的距离为![]() ,两个三角形重合部分的面积为
,两个三角形重合部分的面积为![]() ,则
,则![]() 关于
关于![]() 的函数图象是( )
的函数图象是( )
A.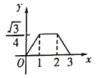 B.
B.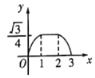 C.
C.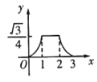 D.
D.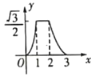
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com