
【题目】定义:若一个三角形一条边上的高等于这条边长的一半,则称该三角形为“半高”三角形,这条高称为“半高”.

(1)如图1,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 求证:
求证: ![]() 是“半高”三角形;
是“半高”三角形;
(2)如图2,![]() 是“半高”三角形,且
是“半高”三角形,且![]() 边上的高是“半高”,点
边上的高是“半高”,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
①请探究![]() ,
,![]() ,
,![]() 之间的等量关系,并说明理由;
之间的等量关系,并说明理由;
②若![]() 的面积等于16,求
的面积等于16,求![]() 的最小值.
的最小值.
【答案】(1)证明见解析;(2)①![]() ;②
;②![]() 取得最小值
取得最小值![]() .
.
【解析】
(1)根据平行相似,证明![]() ,利用相似三角形对应边的比等于对应高的比:
,利用相似三角形对应边的比等于对应高的比:![]() ,由“半高”三角形的定义可结论;
,由“半高”三角形的定义可结论;
(2)证明四边形![]() 是矩形,得
是矩形,得![]() ,代入
,代入![]() ,可得结论;
,可得结论;
(3)先根据△ABC的面积等于16,计算BC和AR的长,设MN=x,则![]() ,根据勾股定理表示MQ,配方可得最小值
,根据勾股定理表示MQ,配方可得最小值
解:(1)证明:由题意可证得![]() ,
,
∴![]() ,
,
∴![]() ,
,
由题意可证得四边形![]() 为矩形,∴
为矩形,∴![]() ,
,
∴![]() ,
,
∴![]() 是“半高”三角形.
是“半高”三角形.
(2)①![]() .理由如下:
.理由如下:
如图,过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,
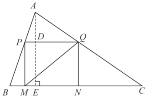
∵![]() 是“半高”三角形,且
是“半高”三角形,且![]() 边上的高是“半高”,
边上的高是“半高”,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由题意可证得四边形![]() 是矩形,有
是矩形,有![]() ,
,![]() ,
,
∴![]() ,
,
即![]() .
.
②∵![]() ,故
,故![]() ,
,
设![]() ,由①得
,由①得![]() ,
,
∴![]() ,
,
∴当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.


科目:初中数学 来源: 题型:
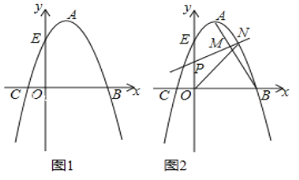
【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
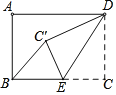
【题目】矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅社有100张床位,若每张床位每晚收费100元,床位可全部租出,若每张床位每晚收费提高20元,则减少10张床位租出;若每张床位每晚收费再提高20元,则再减少10张床位租出.以每次提高20元的这种方法变化下去,为了投资少而收入最多,每张床位每晚应提高( )
A.60元B.50元C.40元D.40元或60元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O.
(1)若∠OAB=25°,求∠APB的度数;
(2)若∠OAB=n°,请直接写出∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张正面标有数字![]() ,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
,背面颜色一样的卡片,正面朝下放在桌面上,小红从中随机抽取一张卡片记下数字,再从余下的卡片中随机抽取一张卡片记下数字.
(1)第一次抽到数字2的卡片的概率是 ;
(2)设第一次抽到的数字为![]() ,第二次抽到的数字为
,第二次抽到的数字为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,请用树状图或列表法求点
,请用树状图或列表法求点![]() 在第三象限的概率.
在第三象限的概率.
![]()
![]()
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一项工程,乙队单独完成所需的时间是甲队单独完成所需时间的2倍,若两队合作4天后,剩下的工作甲单独做还需要6天完成.
(1)求甲、乙两队单独完成这项工程各需多少天;
(2)若甲队每天的报酬是1万元,乙队每天的报酬是0.3万元,要使完成这项工程时的总报酬不超过9.6万元,甲队最多可以工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com