
【题目】矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为_____.
【答案】2或5.
【解析】
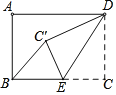
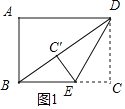
分情况讨论:当∠BC′E=90°时,如图1;当∠BEC′=90°时,如图2,分别利用矩形的性质和勾股定理进行计算即可.
解:如图1,当∠BC′E=90°时,
在矩形ABCD中,AB=6,AD=BC=8,
∴BD=10,
∵把△DCE沿DE折叠,使点C落在点C′处,
∴∠DC′E=∠C=90°,
∵∠BC′E=90°,
∴B,C′,D三点共线,
∴DC′=DC=6,
∴BC′=4,BE=8﹣C′E,
∵BC′2+EC′2=BE2,
∴42+C′E2=(8﹣C′E)2,
解得C′E=3,
∴BE=8﹣3=5;
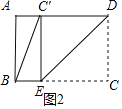
如图2,当∠BEC′=90°时,
在矩形ABCD中,AB=CD=6,AD=BC=8,
∵把△DCE沿DE折叠,使点C落在点C′处,
∴∠DC′E=∠C=90°,
∵∠BEC′=90°,
∴∠CEC′=90°,
∵CD=C′D,
∴四边形ECDC′是正方形,
∴C′E=CE=CD=6,
∴BE=8-6=2.
综上所述,当△BEC′为直角三角形时,BE的长为2或5,
故答案为:2或5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
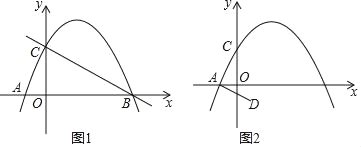
【题目】已知:抛物线y=﹣![]() x2+bx+c交x轴于点A(﹣1,0)和点B,交y轴于点C(0,2)
x2+bx+c交x轴于点A(﹣1,0)和点B,交y轴于点C(0,2)
(1)求抛物线的表达式;
(2)点P为第一象限抛物线上一点,是否存在使△PBC面积最大的点P?若不存在,请说明理由;若存在,求出点P的坐标;
(3)点D坐标为(1,﹣1),连接AD,将线段AD绕平面内某一点旋转180度得线段MN(点M、N分别与点A、D对应),使点M、N都在抛物线上,求点M、N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝重庆南开中学建校83周年暨校运动会,我校初二(21)班准备统一穿初一时期订制的服装参加运动会,分别需要增订“英伦学院风”班服(250元/件)、“![]() ”运动裤(90元/件)、“少年的我”短袖
”运动裤(90元/件)、“少年的我”短袖![]() 恤(40元/件)共50件(三种服装均有增订),总花费6000元,且需要增订“少年的我”短袖
恤(40元/件)共50件(三种服装均有增订),总花费6000元,且需要增订“少年的我”短袖![]() 恤的件数最多,则需要增订“
恤的件数最多,则需要增订“![]() ”运动裤__________件.
”运动裤__________件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保障国庆70周年南口阅兵训练基地全体人员的生活,需通过铁路、公路两种运输方式运送生活物资.原计划铁路运输物资的5倍是公路运输的8倍,实际铁路运输的物资减少了15吨,公路运输增加了15吨,且铁路运输物资的2倍比公路运输的3倍少60吨.
(1)原计划铁路、公路分别运输多少吨物资到训练基地?
(2)现采用微型集装箱装载这些物资,每个集装箱装满后箱货总重量为1.6吨,空箱重量为0.1吨.为增加集装箱的载货量将其进行改造,改造后每个集装箱装满后箱货总重量比改造前增加![]() 吨,空箱重量比改造前减少
吨,空箱重量比改造前减少![]() 吨,其中
吨,其中![]() .改造前的集装箱每个装满后恰好装下这些物资.若用改造后的集装箱来装载这些物资,改造后的集装箱个数比改造前少用10个.设改造后的集装箱最大载货量总重量为
.改造前的集装箱每个装满后恰好装下这些物资.若用改造后的集装箱来装载这些物资,改造后的集装箱个数比改造前少用10个.设改造后的集装箱最大载货量总重量为![]() 吨,求
吨,求![]() 关于
关于![]() 的函数关系式以及
的函数关系式以及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组,对函数y=|x﹣1|+1的图象和性质进行了探究,探究过程如下:
(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | … |
其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
(3)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x=1的右侧,函数图象呈上升状态 | 当x>1时,y随x的增大而增大 |
① | 在直线x=1的左侧,函数图象呈下降状态 |
|
示例2 | 函数图象经过点(﹣3,5) | 当x=﹣3时,y=5 |
② | 函数图象的最低点是(1,1) |
|
(4)当2<y≤4时,x的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
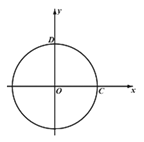
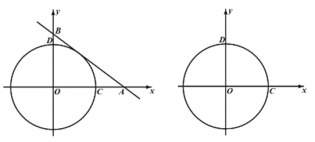
【题目】如图,在平面直角坐标系xOy中,一次函数y=-![]() +b(b>0,b为常数)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴交于点C,与y轴正半轴相交于点D.
+b(b>0,b为常数)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴交于点C,与y轴正半轴相交于点D.
(1)若直线AB与⊙O相切于弧CD上一点,求b的值;
(2)若直线AB与⊙O有两个交点F、G.
①b为何值时,⊙O上有且只有3个点到直线AB的距离为2?并求出此时直线被⊙O所截的弦FG的长;
②是否存在这样的b,使得∠GOF=90°?若存在,求出b的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )

A.①②B.②③C.①③D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com