
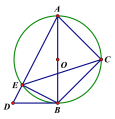
【题目】如图,已知以AB为直径的圆中,∠ACB=∠ABD=90°,∠D=60°,∠ABC=45°.
(1)求证:EC平分∠AEB;
(2)求![]() 的值.
的值.
【答案】(1)见详解;(2)![]() .
.
【解析】
由Rt△ACB中∠ABC=45°,得出∠BAC=∠ABC=45°,根据圆周角定理得出∠AEC=∠ABC,∠BEC=∠BAC,等量代换得出∠AEC=∠BEC,即EC平分∠AEB;
(2)方法1、设AB与CE交于点M.根据角平分线的性质得出![]() =
=![]() .易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=
.易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE= ![]() BE,那么
BE,那么![]() =
=![]() =
= ![]() .作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出
.作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出 ![]() =
= ![]() =
=![]() ,进而求出
,进而求出 ![]() =
= ![]() =
=![]() =
=![]() .
.
方法2、易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=![]() BE,那么
BE,那么 ![]() =
=![]() =
= ![]() ,再用角平分线定理判断出CP=CQ,即可得出结论.
,再用角平分线定理判断出CP=CQ,即可得出结论.
(1)证明:∵Rt△ACB中,∠ACB=90°,∠ABC=45°,
∴∠BAC=∠ABC=45°,
∵∠AEC=∠ABC,∠BEC=∠BAC,
∴∠AEC=∠BEC,
即EC平分∠AEB;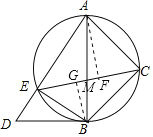 (2)解:如图,设AB与CE交于点M.
(2)解:如图,设AB与CE交于点M.
∵EC平分∠AEB,
∴ ![]() =
=![]() .
.
在Rt△ABD中,∠ABD=90°,∠D=60°,
∴∠BAD=30°,
∵以AB为直径的圆经过点E,
∴∠AEB=90°,
∴tan∠BAE= ![]() =
=![]() ,
,
∴AE=![]() BE,
BE,
∴ ![]() =
=![]() =
= ![]() .
.
作AF⊥CE于F,BG⊥CE于G.
在△AFM与△BGM中,
∵∠AFM=∠BGM=90°,∠AMF=∠BMG,
∴△AFM∽△BGM,
∴![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
=![]() =
=![]() .
.
方法2、如图1,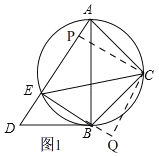
在Rt△ABD中,∠ABD=90°,∠D=60°,
∴∠BAD=30°,
∵以AB为直径的圆经过点E,
∴∠AEB=90°,
∴tan∠BAE= ![]() =
=![]() ,
,
∴ AE= ![]() BE,
BE,
过点C作CP⊥AE于P,过点C作CQ⊥EB交延长线于Q,
由(1)知,EC是∠AEB的角平分线,
∴CP=CQ,
∴ ![]() =
= ![]() =
= ![]() =
= ![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,3),B(2,5),C(4,2)(每个方格的边长均为1个单位长度)
(1)将△ABC平移,使点A移动到点A1,请画出△A1B1C1;
(2)作出△ABC关于O点成中心对称的△A2B2C2,并直接写出A2,B2,C2的坐标;
(3)△A1B1C1与△A2B2C2是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
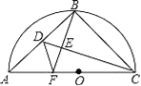
【题目】如图,半圆O的直径AC=2![]() ,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为_____.
,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距160千米,一辆公共汽车从
两地相距160千米,一辆公共汽车从![]() 地出发,开往
地出发,开往![]() 地,2小时后,又从
地,2小时后,又从![]() 地同方向开出一辆小汽车,小汽车的速度是公共汽车的3倍,结果小汽车比公共汽车早到40分钟到达
地同方向开出一辆小汽车,小汽车的速度是公共汽车的3倍,结果小汽车比公共汽车早到40分钟到达![]() 地,求两种车的速度?
地,求两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交y轴于B(0,﹣4),则四边形AOBC的面积为_____.
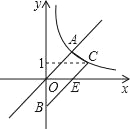
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用4个全等的直角三角形与1个小正方形镶嵌而成的正方图案,已知大正方形面积为10,小正方形面积为2,若用![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中说法正确的有____________.(只填序号)
.其中说法正确的有____________.(只填序号)
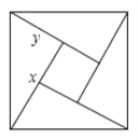
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为_____.
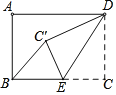
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com