
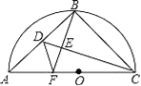
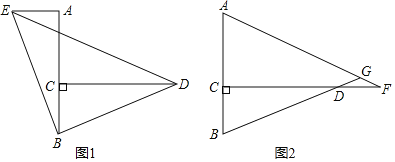
【题目】如图,半圆O的直径AC=2![]() ,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为_____.
,点B为半圆的中点,点D在弦AB上,连结CD,作BF⊥CD于点E,交AC于点F,连结DF,当△BCE和△DEF相似时,BD的长为_____.
【答案】![]()
【解析】
分两种情形讨论:①当∠DFE=∠BCE时,可以证明DB=DC,BC=CF,∠DFC=∠DBC=90°即可解决问题.②当∠FDE=∠BCE时,可以证明DF∥BC、△BDF∽△CBD得到![]() =
=![]() 列出方程解决问题.
列出方程解决问题.
解: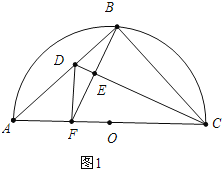
①如图1,当∠DFE=∠BCE时,
∵∠DEF=∠BEC,
∴△DEF∽△BEC,
∵AC是直径,
∴∠ABC=90°,
∵BF⊥CD,
∴∠CEB=90°,
∴∠BCE+∠CBE=90°,∠DBE+∠EBC=90°,
∴∠DBE=∠BCE=∠DFE,
∴DB=DF,
∵DE⊥BF,
∴EB=EF,
∴BC=CF,
∵点B为半圆的中点,
∴AB=BC,
∴∠A=45°,
∵∠DBF=∠DFB,∠CBF=∠CFB,∠DBF+∠CBF=90°,
∴∠DFB+∠CFB=90°,
∴∠DFC=∠DFA=90°,
∴∠A=∠ADF=45°,
∴AF=DF=BD,
在RT△ABC中,∵AC=2![]() ,
,
∴AB=BC=![]() AC=2,
AC=2,
∴FC=2,
∴BD=AF=AC-FC=2![]() -2,
-2,
②如图2,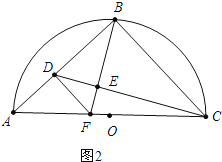
当∠FDE=∠BCE时,
∵∠DEF=∠BEC,
∴△DEF∽△CEB,DF∥BC,
∴∠ADF=∠ABC=90°,
∵∠ABC=∠BEC=90°,
∴∠BCE+∠CBE=90°,∠DBE+∠EBC=90°,
∴∠DBE=∠BCE=∠FDE,
∵∠BDF=∠DBC=90°,∠DBF=∠BCD,
∴△BDF∽△CBD,
∴![]() =
=![]() ,
,
∵∠A=45°,∠ADF=90°,
∴∠AFD=∠A=45°,
∴AD=DF,
设BD=x,由(1)可知:AB=BC=2,AD=DF=2-x,
∴![]() =
=![]() ,整理得:x2+2x-4=0,
,整理得:x2+2x-4=0,
解得:x= -1+![]() (或-1-
(或-1-![]() 舍弃)
舍弃)
∴BD=![]() -1.
-1.
故答案为2![]() -2或
-2或![]() -1.
-1.


科目:初中数学 来源: 题型:
【题目】如图1是一座立交桥的示意图(道路宽度忽略不计), A为入口, F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF ;弯道为以点O为圆心的一段弧,且弧BC,弧ED,弧CD所对的圆心角均为90°.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出. 其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法错误的是( )

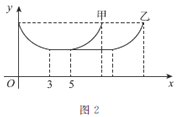
A. 甲车在立交桥上共行驶8s B. 从F口出比从G口出多行驶40m
C. 甲车从F口出,乙车从G口出 D. 立交桥总长为150m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为![]() .
.
(1)求线段AP的长;
(2)若DE是⊙O的切线,求线段OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
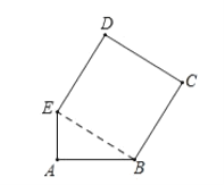
【题目】如图1,已知AB⊥CD,C是AB上一动点,AB=CD
(1)在图1中,将BD绕点B逆时针方向旋转90°到BE,若连接DE,则△DBE为等腰直角三角形;若连接AE,试判断AE与BC的数量和位置关系并证明;
(2)如图2,F是CD延长线上一点,且DF=BC,直线AF,BD相交于点G,∠AGB的度数是一个固定值吗?若是,请求出它的度数;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场开展购物抽奖活动,抽奖箱中有3个形状、大小和质地等完全相同的小球,分别标有数字1、2、3.顾客从中随机摸出一个小球,然后放回箱中,再随机摸出一个小球.
(1)利用树形图法或列表法(只选其中一种),表示摸出小球可能出现的所有结果;
(2)若规定:两次摸出的小球的数字之积为9,则为一等奖;数字之积为6,则为二等奖;数字之积为2或4,则为三等奖.请你分别求出顾客抽中一等奖、二等奖、三等奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,五边形![]() 是学校的一块种植基地示意图,这块基地可以分成正方形
是学校的一块种植基地示意图,这块基地可以分成正方形![]() 和
和![]() ,已知这个五边形的周长为88米,正方形
,已知这个五边形的周长为88米,正方形![]() 的面积为400平方米.
的面积为400平方米.
(1)求正方形![]() 的周长;
的周长;
(2)求点![]() 到
到![]() 边的距离.
边的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝重庆南开中学建校83周年暨校运动会,我校初二(21)班准备统一穿初一时期订制的服装参加运动会,分别需要增订“英伦学院风”班服(250元/件)、“![]() ”运动裤(90元/件)、“少年的我”短袖
”运动裤(90元/件)、“少年的我”短袖![]() 恤(40元/件)共50件(三种服装均有增订),总花费6000元,且需要增订“少年的我”短袖
恤(40元/件)共50件(三种服装均有增订),总花费6000元,且需要增订“少年的我”短袖![]() 恤的件数最多,则需要增订“
恤的件数最多,则需要增订“![]() ”运动裤__________件.
”运动裤__________件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com