
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨°˜ABCµƒ»˝∏ˆ∂•µ„◊¯±Í∑÷±Œ™A£®1£¨3£©£¨B£®2£¨5£©£¨C£®4£¨2£©£®√ø∏ˆ∑Ω∏Òµƒ±þ≥§æ˘Œ™1∏ˆµ•Œª≥§∂»£©
£®1£©Ω´°˜ABC∆Ω“∆£¨ πµ„A“∆∂ØµΩµ„A1£¨«Îª≠≥ˆ°˜A1B1C1£ª
£®2£©◊˜≥ˆ°˜ABCπÿ”⁄Oµ„≥…÷––ƒ∂‘≥∆µƒ°˜A2B2C2£¨≤¢÷±Ω”–¥≥ˆA2£¨B2£¨C2µƒ◊¯±Í£ª
£®3£©°˜A1B1C1”ΰ˜A2B2C2 «∑Ò≥…÷––ƒ∂‘≥∆£ø»Ù «£¨«Î–¥≥ˆ∂‘≥∆÷––ƒµƒ◊¯±Í£ª»Ù≤ª «£¨«ÎÀµ√˜¿Ì”…£Æ

°æ¥∞∏°ø£®1£©º˚Ω‚Œˆ£ª£®2£©º˚Ω‚Œˆ£¨µ„A2£¨B2£¨C2µƒ◊¯±Í∑÷±Œ™£®©Å1£¨©Å3£©£¨£®©Å2£¨©Å5£©£¨£®©Å4£¨©Å2£©£ª£®3£© «£¨∂‘≥∆÷––ƒµƒ◊¯±Íµƒ◊¯±ÍŒ™£®©Å2£¨©Å1£©£Æ
°æΩ‚Œˆ°ø
£®1£©¿˚”√µ„A∫Õ![]() ◊¯±Íµƒπÿœµ»∑∂®∆Ω“∆µƒ∑ΩœÚ”Îæý¿Î£¨πÿ”⁄¿˚”√¥À∆Ω“∆πʬ…–¥≥ˆB1°¢C1µƒ◊¯±Í£¨»ª∫Û√˵„º¥ø…£ª
◊¯±Íµƒπÿœµ»∑∂®∆Ω“∆µƒ∑ΩœÚ”Îæý¿Î£¨πÿ”⁄¿˚”√¥À∆Ω“∆πʬ…–¥≥ˆB1°¢C1µƒ◊¯±Í£¨»ª∫Û√˵„º¥ø…£ª
(2)¿˚”√πÿ”⁄µ„∂‘≥∆µƒµ„µƒ◊¯±ÍÃÿ’˜–¥≥ˆA2£¨B2£¨C2µƒ◊¯±Í£¨»ª∫Û√˵„º¥ø…£ª
(3£©¡¨Ω”A1 A2£¨B1 B2£¨C1 C2£¨À¸√«∂ºæ≠π˝µ„P£¨¥”∂¯ø…≈–∂œ°˜A1B1C1”ΰ˜A2B2C2πÿ”⁄µ„P÷––ƒ∂‘≥∆£¨‘Ÿ–¥≥ˆPµ„◊¯±Íº¥ø…£Æ
Ω‚£∫£®1£©»ÁÕº£¨°˜A1B1C1Œ™À˘◊˜£ª
£®2£©»ÁÕº£¨°˜A2B2C2Œ™À˘◊˜£ªµ„A2£¨B2£¨C2µƒ◊¯±Í∑÷±Œ™£®©Å1£¨©Å3£©£¨£®©Å2£¨©Å5£©£¨£®©Å4£¨©Å2£©£ª

£®3£©°˜A1B1C1”ΰ˜A2B2C2πÿ”⁄µ„P÷––ƒ∂‘≥∆£¨»ÁÕº£¨
∂‘≥∆÷––ƒµƒ◊¯±Íµƒ◊¯±ÍŒ™£®©Å2£¨©Å1£©£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ҃ͣ¨6‘¬12»’Œ™∂ÀŒÁΩ⁄£Æ‘⁄∂ÀŒÁΩ⁄«∞œ¶£¨»˝ŒªÕ¨—ßµΩƒ≥≥¨ –µ˜—–“ª÷÷Ω¯º€Œ™2‘™µƒÙ’◊”µƒœ˙ €«Èøˆ£Æ«Î∏˘æð–°¿ˆÃ·π©µƒ–≈œ¢£¨Ω‚¥–°ª™∫Õ–°√˜Ã·≥ˆµƒŒ £Æ

£®1£©–°ª™µƒŒ Ã‚Ω‚¥£∫°°°°°°°°£ª
£®2£©–°√˜µƒŒ Ã‚Ω‚¥£∫°°°°°°°°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨°˜ACD∫Õ°˜AEB∂º «µ»—¸÷±Ω«»˝Ω«–Œ£¨°œCAD=°œEAB=90°„£¨Àƒ±þ–ŒABCD «∆Ω––Àƒ±þ–Œ£¨œ¬¡–Ω·¬€¥ÌŒÛµƒ «£® £©
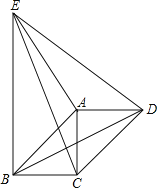
A. —ÿAEÀ˘‘⁄÷±œþ’€µ˛∫Û£¨°˜ACE∫Õ°˜ADE÷ÿ∫œ
B. —ÿADÀ˘‘⁄÷±œþ’€µ˛∫Û£¨°˜ADB∫Õ°˜ADE÷ÿ∫œ
C. “‘AŒ™–˝◊™÷––ƒ£¨∞—°˜ACEƒÊ ±’Ζ˝◊™90°„∫۔ΰ˜ADB÷ÿ∫œ
D. “‘AŒ™–˝◊™÷––ƒ£¨∞—°˜ACBƒÊ ±’Ζ˝◊™270°„∫۔ΰ˜DAC÷ÿ∫œ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
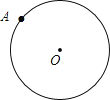
°æƒø°ø»ÁÕº£¨µ„A «∞Îæ∂Œ™3µƒ°—O…œµƒµ„£¨
![]() ≥þπÊ◊˜Õº£∫◊˜°—Oµƒƒ⁄Ω”’˝¡˘±þ–ŒABCDEF£ª
≥þπÊ◊˜Õº£∫◊˜°—Oµƒƒ⁄Ω”’˝¡˘±þ–ŒABCDEF£ª
![]() «Û
«Û![]() ÷–ª°ACµƒ≥§£Æ
÷–ª°ACµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø≈◊ŒÔœþ![]() µƒ∂•µ„Œ™
µƒ∂•µ„Œ™![]() £¨”Îx÷·µƒ“ª∏ˆΩªµ„A‘⁄µ„
£¨”Îx÷·µƒ“ª∏ˆΩªµ„A‘⁄µ„![]() ∫Õ
∫Õ![]() ÷ƺ‰£¨∆‰≤ø∑÷ÕºœÛ»ÁÕº£¨∆‰÷–¥ÌŒÛµƒΩ·¬€Œ™
÷ƺ‰£¨∆‰≤ø∑÷ÕºœÛ»ÁÕº£¨∆‰÷–¥ÌŒÛµƒΩ·¬€Œ™![]()
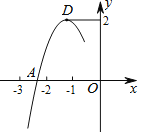
A. ∑Ω≥Ã![]() µƒ∏˘Œ™
µƒ∏˘Œ™![]() B.
B. ![]()
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®∏≈ƒÓ—ßœ∞£©
πÊ∂®£∫«Û»Ù∏…∏ˆœýÕ¨µƒ”–¿Ì ˝£®æ˘≤ªµ»”⁄0£©µƒ≥˝∑®‘ÀÀ„Ω–◊ˆ≥˝∑Ω£¨»Á2°¬2°¬2£¨£®©Å3£©°¬£®©Å3£©°¬£®©Å3£©°¬£®©Å3£©µ»£Æ¿ý±»”–¿Ì ˝µƒ≥À∑Ω£¨Œ“√«∞—2°¬2°¬2º«◊˜2¢€£¨∂¡◊˜°∞2µƒ»¶3¥Œ∑Ω°±£¨£®©Å3£©°¬£®©Å3£©°¬£®©Å3£©°¬£®©Å3£©º«◊˜£®©Å3£©¢Ð£¨∂¡◊˜°∞©Å3µƒ»¶4¥Œ∑Ω°±£¨“ª∞„µÿ£¨∞— ![]() £®a°Ÿ0£©º«◊˜a£¨∂¡◊˜°∞aµƒ»¶n¥Œ∑Ω°±£Æ
£®a°Ÿ0£©º«◊˜a£¨∂¡◊˜°∞aµƒ»¶n¥Œ∑Ω°±£Æ
£®1£©£®≥ı≤ΩÃΩæø£©
÷±Ω”–¥≥ˆº∆À„Ω·π˚£∫2¢€=_______£¨£®-![]() £©¢ð=_______£ª
£©¢ð=_______£ª
£®2£©£®…Ó»ÎÀºøº£©
Œ“√«÷™µ¿£¨”–¿Ì ˝µƒºı∑®‘ÀÀ„ø…“‘◊™ªØŒ™º”∑®‘ÀÀ„£¨≥˝∑®‘ÀÀ„ø…“‘◊™ªØŒ™≥À∑®‘ÀÀ„£¨”–¿Ì ˝µƒ≥˝∑Ω‘ÀÀ„»Á∫Œ◊™ªØŒ™≥À∑Ω‘ÀÀ„ƒÿ£ø
¢Ò. ‘“ª ‘£∫∑¬’’…œ√ʵƒÀ„ Ω£¨Ω´œ¬¡–‘ÀÀ„Ω·π˚÷±Ω”–¥≥…√𵃖Œ Ω£Æ
£®©Å3£©¢Ð=_______£ª5¢Þ=_______£ª (-![]() ) ¢‚=_______£Æ
) ¢‚=_______£Æ
¢Ú. œÎ“ªœÎ£∫Ω´“ª∏ˆ∑«¡„”–¿Ì ˝aµƒ»¶n¥Œ∑Ω–¥≥…√𵃖Œ Ωµ»”⁄_______£ª
¢Û. À„“ªÀ„£∫
12°¬(-![]() )¢Ð°¡(-2)¢ð£≠(-
)¢Ð°¡(-2)¢ð£≠(-![]() )¢Þ°¬3.
)¢Þ°¬3.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨“—÷™°œC=90°„£¨°œA=60°„£¨AC=3cm£¨“‘–±±þABµƒ÷–µ„PŒ™–˝◊™÷––ƒ£¨∞—’‚∏ˆ»˝Ω«–Œ∞¥ƒÊ ±’Î∑ΩœÚ–˝◊™90°„µ√µΩRt°˜A°‰B°‰C°‰£¨‘Ú–˝◊™«∞∫Û¡Ω∏ˆ÷±Ω«»˝Ω«–Œ÷ÿµ˛≤ø∑÷µƒ√ʪ˝Œ™______________£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ˙«Ï∑≈ºŸ ±£¨–°√˜“ªº“»˝ø⁄“ª∆≥À–°ΩŒ≥µ»•œÁœ¬ÃΩÕ˚“ؓذ¢ƒÃƒÃ∫ÕÕ‚π´°¢Õ‚∆≈°£‘Á…œ¥”º“¿Ô≥ˆ∑¢£¨œÚ∂´◊þ¡À6«ß√◊µΩ≥¨ –¬Ú∂´Œ˜£¨»ª∫Û”÷œÚ∂´◊þ¡À1.5«ß√◊µΩ“ؓغ“£¨÷–ŒÁ¥”“ؓغ“≥ˆ∑¢œÚŒ˜◊þ¡À12«ß√◊µΩÕ‚π´º“£¨ÕÌ…œ∑µªÿº“¿Ô°£
£®1£©»Ù“‘º“Œ™‘≠µ„£¨œÚ∂´Œ™’˝∑ΩœÚ£¨”√1∏ˆµ•Œª≥§∂»±Ì æ1«ß√◊£¨«ÎΩ´≥¨ –°¢“ؓغ“∫ÕÕ‚π´º“µƒŒª÷√‘⁄œ¬√Ê ˝÷·…œ∑÷±”√µ„A°¢B°¢C±Ì æ≥ˆ¿¥£ª
![]()
£®2£©Œ ≥¨ –A∫ÕÕ‚π´º“Cœýæý∂ý…Ÿ«ß√◊£ø
£®3£©»Ù–°ΩŒ≥µ√ø«ß√◊∫ƒ”Õ0.08…˝£¨«Û–°√˜“ªº“¥”≥ˆ∑¢µΩ∑µªÿº“À˘æ≠¿˙¬∑≥Ö°≥µµƒ∫ƒ”Õ¡ø°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∞—œ¬√ʵƒ”–¿Ì ˝ÃÓ‘⁄œý”¶µƒ¥Û¿®∫≈¿Ô£∫£®°Ô”—«È÷ æ£∫Ω´∏˜ ˝”√∂∫∫≈∑÷ø™£©
15£¨£≠![]() £¨ 0£¨£≠0.15£¨ £≠128£¨
£¨ 0£¨£≠0.15£¨ £≠128£¨ ![]() £¨£´20£¨£≠2.6
£¨£´20£¨£≠2.6
’˝ ˝ºØ∫œ { . . . ©y£ª
∏∫ ˝ºØ∫œ ©x . . . ©y£ª
’˚ ˝ºØ∫œ ©x°° . . . ©y£ª
∑«∏∫ ˝ºØ∫œ ©x . . . ©y£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com