
【题目】如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是( )
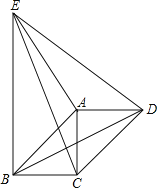
A. 沿AE所在直线折叠后,△ACE和△ADE重合
B. 沿AD所在直线折叠后,△ADB和△ADE重合
C. 以A为旋转中心,把△ACE逆时针旋转90°后与△ADB重合
D. 以A为旋转中心,把△ACB逆时针旋转270°后与△DAC重合
【答案】D
【解析】试题解析:A、由于△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,则AD=AC,∠BAC=45°,于是∠EAD=135°,∠CAE=135°,所以△ACE≌△ADE,所以A选项的结论正确;
B、由于△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,则AB=AE,∠BAC=45°,于是∠BAD=135°,∠DAE=135°,所以△ADB≌△ADE,所以B选项的结论正确;
C、由A、B选项得到∠CAD=90°,∠BAE=90°,AB=AE,AD=AC,所以以A为旋转中心,把△ACE逆时针旋转90°后与△ADB重合,所以C选项的结论正确;
D、由于四边形ABCD是平行四边形,则△ACB与△DAC为全等的等腰直角三角形,△ACB与△DAC只能经过翻折和平移才能重合,所以D选项的结论错误.
故选D.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在两个不透明的口袋中分别装有三个颜色分别为红色、白色、绿色的小球,这三个小球除颜色外其他都相同,
(1)在其中一个口袋中一次性随机摸出两个球,请写出在这一过程中的一个必然事件;
(2)若分别从两个袋中随机取出一个球,试求出两个小球颜色相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表) 甲超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 5 | 10 | 5 |
乙超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 10 | 5 | 10 |
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ADB和△ADC中,下列条件:①BD=DC,AB=AC;②∠B=∠C,∠BAD=∠CAD;③∠B=∠C,BD=DC;④∠ADB=∠ADC,BD=DC.能得出△ADB≌△ADC的序号是 .
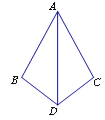
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
![]() ……
……
(1)请写出第4个等式:________________;
(2)观察上述等式的规律,猜想第n个等式(用含n的式子表示),并验证其正确性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com