
【题目】如图,AB、AC是⊙O的两条弦∠A=25°,过点C的切线与OB的延长线交于点D,则∠D的度数是 . 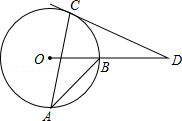
科目:初中数学 来源: 题型:
【题目】(1)通过计算下列各式的值探究问题:
①![]() = ;
= ;![]() = ;
= ;![]() = ;
= ;![]() = .
= .
探究:对于任意非负有理数a,![]() = .
= .
②![]() = ;
= ;![]() = ;
= ;![]() = ;
= ;![]() = .
= .
探究:对于任意负有理数a,![]() = .
= .
综上,对于任意有理数a,![]() = .
= .
(2)应用(1)所得的结论解决问题:有理数a,b在数轴上对应的点的位置如图所示,化简:![]() -
-![]() -
-![]() +|a+b|.
+|a+b|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校想了解学生每周的课外阅读时间情况,随机调查了部分学生,对学生每周的课外阅读时间x(单位:小时)进行分组整理,并绘制了如图所示的不完整的频数分别直方图和扇形统计图:

根据图中提供的信息,解答下列问题:
(1)补全频数分布直方图
(2)求扇形统计图中m的值和E组对应的圆心角度数
(3)请估计该校3000名学生中每周的课外阅读时间不小于6小时的人数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=20°,∠AOE=86°,OB平分∠AOC,OD平分∠COE.
(1)∠COD的度数是______;
(2)若以O为观察中心,OA为正东方向,射线OD在什么位置?
(3)若以OA为钟面上的时针,OD为分针,且OA正好在“时刻3”的下方不远,求出此时的时刻.(结果精确到分钟)
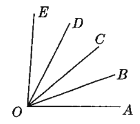
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减轻学生课业负担,提高课堂效果,我县教体局积极推进 “高效课堂”建设.
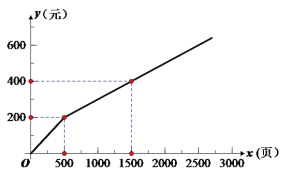
某学校的《课堂检测》印刷任务原来由甲复印店承接,其每月收费y(元)与复印页数x(页)的函数关系如图所示:
⑴从图象中可看出:每月复印超过500页部分每页收费 元;
⑵现在乙复印店表示:若学校先按每月付给200元的月承包费,则可按每页0.15元收费.乙复印店每月收费y(元)与复印页数x(页)的函数关系为 ;
⑶在给出的坐标系内画出(2)中的函数图象,并结合函数图象回答每月复印在3000页左右应选择哪个复印店?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACD和△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,四边形ABCD是平行四边形,下列结论错误的是( )
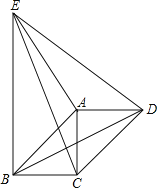
A. 沿AE所在直线折叠后,△ACE和△ADE重合
B. 沿AD所在直线折叠后,△ADB和△ADE重合
C. 以A为旋转中心,把△ACE逆时针旋转90°后与△ADB重合
D. 以A为旋转中心,把△ACB逆时针旋转270°后与△DAC重合
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠CAB=90°,AD⊥BC于点D,点E为AB的中点,EC与AD交于点G,点F在BC上.
(1)如图1,AC:AB=1:2,EF⊥CB,求证:EF=CD. 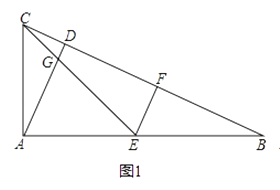
(2)如图2,AC:AB=1: ![]() ,EF⊥CE,求EF:EG的值.
,EF⊥CE,求EF:EG的值. 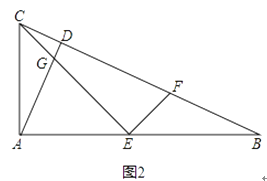
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离 ![]() (千米)与时间
(千米)与时间 ![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点 ![]() ,点
,点 ![]() 坐标为
坐标为 ![]() ,曲线
,曲线 ![]() 可用二次函数
可用二次函数 ![]() (
( ![]() ,
, ![]() 是常数)刻画.
是常数)刻画.
(1)求 ![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以 ![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为 ![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度 ![]() ,
, ![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com