
【题目】为保障国庆70周年南口阅兵训练基地全体人员的生活,需通过铁路、公路两种运输方式运送生活物资.原计划铁路运输物资的5倍是公路运输的8倍,实际铁路运输的物资减少了15吨,公路运输增加了15吨,且铁路运输物资的2倍比公路运输的3倍少60吨.
(1)原计划铁路、公路分别运输多少吨物资到训练基地?
(2)现采用微型集装箱装载这些物资,每个集装箱装满后箱货总重量为1.6吨,空箱重量为0.1吨.为增加集装箱的载货量将其进行改造,改造后每个集装箱装满后箱货总重量比改造前增加![]() 吨,空箱重量比改造前减少
吨,空箱重量比改造前减少![]() 吨,其中
吨,其中![]() .改造前的集装箱每个装满后恰好装下这些物资.若用改造后的集装箱来装载这些物资,改造后的集装箱个数比改造前少用10个.设改造后的集装箱最大载货量总重量为
.改造前的集装箱每个装满后恰好装下这些物资.若用改造后的集装箱来装载这些物资,改造后的集装箱个数比改造前少用10个.设改造后的集装箱最大载货量总重量为![]() 吨,求
吨,求![]() 关于
关于![]() 的函数关系式以及
的函数关系式以及![]() 的最大值.
的最大值.
【答案】(1)原计划铁路、公路分别运输120吨,75吨物资到训练基地;(2)w=132m+180,w最大值为232.8吨.
【解析】
(1)设原计划铁路、公路分别运输a吨,b吨物资到训练基地,根据“原计划铁路运输物资的5倍是公路运输的8倍,实际铁路运输的物资减少了15吨,公路运输增加了15吨,且铁路运输物资的2倍比公路运输的3倍少60吨”列出方程组,求解即可;
(2)首先求出改造前的集装箱的个数,然后列出w关于m的函数关系式,利用一次函数的性质求解.
解:(1)设原计划铁路、公路分别运输a吨,b吨物资到训练基地,
由题意得: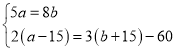 ,
,
解得:![]() ,
,
答:原计划铁路、公路分别运输120吨,75吨物资到训练基地;
(2)改造前的集装箱的个数为:![]() =130个,
=130个,
由题意可得:w=(13010)[(1.6+m)(0.1![]() )]=132m+180,
)]=132m+180,
∴w随m的增大而增大,
∵0.1≤m≤0.4.
∴当m=0.4时,w最大值=232.8吨.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】![]() 、
、![]() 两地相距160千米,一辆公共汽车从
两地相距160千米,一辆公共汽车从![]() 地出发,开往
地出发,开往![]() 地,2小时后,又从
地,2小时后,又从![]() 地同方向开出一辆小汽车,小汽车的速度是公共汽车的3倍,结果小汽车比公共汽车早到40分钟到达
地同方向开出一辆小汽车,小汽车的速度是公共汽车的3倍,结果小汽车比公共汽车早到40分钟到达![]() 地,求两种车的速度?
地,求两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
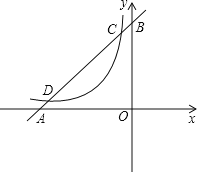
【题目】如图,直线y1=x+m与x轴、y轴交于点A、B,与双曲线![]() 分别交于点C、D,且点C的坐标为(-1,2)
分别交于点C、D,且点C的坐标为(-1,2)
(1)分别求出直线AB及双曲线的解析式;
(2)求出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
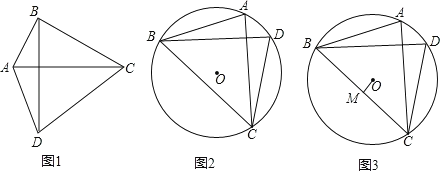
【题目】若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)矩形 “奇妙四边形”(填“是”或“不是”);
(2)如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;
(3)如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )

A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
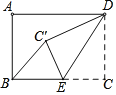
【题目】矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
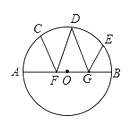
【题目】如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
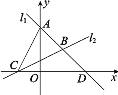
【题目】如图,直线l1过点A(0,4)与点D(4,0),直线l2:y=![]() x+1与x轴交于点C,两直线l1,l2相交于点B.
x+1与x轴交于点C,两直线l1,l2相交于点B.
(1)求直线l1的函数表达式;
(2)求点B的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)为弘扬 “东亚文化”,某单位开展了“东亚文化之都”演讲比赛,在安排1位女选手和3位男选手的出场顺序时,采用随机抽签方式.
(1)请直接写出第一位出场是女选手的概率;
(2)请你用画树状图或列表的方法表示第一、二位出场选手的所有等可能结果,并求出他们都是男选手的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com