
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )

A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=-x2+5x+n经过点A(1,0),与x轴交于点C,与y轴交于点B,顶点为D.
(1)求n的值和D点坐标;
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
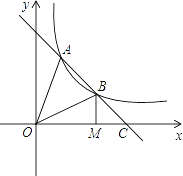
【题目】如图,直线AB交双曲线 ![]() 于A,B两点,交x轴于点C,且BC=
于A,B两点,交x轴于点C,且BC= ![]() AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某校乒乓球队有水平相当的A,B,C,D四名队员.
(1)若将A,B,C,D四名队员随机平均分成甲、乙两组进行乒乓球单打练习,求A、B恰好分在一组的概率.
(2)若从A,B,C,D四名队员中随机抽取两名代表学校参加比赛,求A、B恰好被抽中的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y1=![]() (x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=
(x+1)2+1与y2=a(x﹣4)2﹣3交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于B、C两点,且D、E分别为顶点.则下列结论:①a=![]() ;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2 其中正确结论的个数是( )
;②AC=AE;③△ABD是等腰直角三角形;④当x>1时,y1>y2 其中正确结论的个数是( )

A. 1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保障国庆70周年南口阅兵训练基地全体人员的生活,需通过铁路、公路两种运输方式运送生活物资.原计划铁路运输物资的5倍是公路运输的8倍,实际铁路运输的物资减少了15吨,公路运输增加了15吨,且铁路运输物资的2倍比公路运输的3倍少60吨.
(1)原计划铁路、公路分别运输多少吨物资到训练基地?
(2)现采用微型集装箱装载这些物资,每个集装箱装满后箱货总重量为1.6吨,空箱重量为0.1吨.为增加集装箱的载货量将其进行改造,改造后每个集装箱装满后箱货总重量比改造前增加![]() 吨,空箱重量比改造前减少
吨,空箱重量比改造前减少![]() 吨,其中
吨,其中![]() .改造前的集装箱每个装满后恰好装下这些物资.若用改造后的集装箱来装载这些物资,改造后的集装箱个数比改造前少用10个.设改造后的集装箱最大载货量总重量为
.改造前的集装箱每个装满后恰好装下这些物资.若用改造后的集装箱来装载这些物资,改造后的集装箱个数比改造前少用10个.设改造后的集装箱最大载货量总重量为![]() 吨,求
吨,求![]() 关于
关于![]() 的函数关系式以及
的函数关系式以及![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F分别是矩形ABCD的边AB,AD上的点,∠FEC=∠FCE=45°.
(1)求证:AF=CD.
(2)若AD=3,△EFC的面积为4,求线段BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(多选)在同一条道路上,甲车从![]() 地到
地到![]() 地,乙车从
地,乙车从![]() 地到
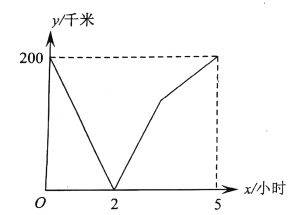
地到![]() 地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离
地,两车同时出发,乙车先到达目的地,图中的折线段表示甲,乙两车之间的距离![]() (千米)与行驶时间
(千米)与行驶时间![]() (小时)的函数关系,下列说法正确的是( )
(小时)的函数关系,下列说法正确的是( )
A.甲乙两车出发2小时后相遇
B.甲车速度是40千米/小时
C.相遇时乙车距离![]() 地100千米
地100千米
D.乙车到![]() 地比甲车到
地比甲车到![]() 地早
地早![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=8,AD=10,点E为BC上一点,将△ABE沿AE折叠,使点B落在长方形内点F处,且DF=6.
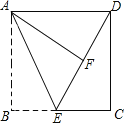
(1)试说明:△ADF是直角三角形;
(2)求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com