
【题目】如图,在长方形ABCD中,AB=8,AD=10,点E为BC上一点,将△ABE沿AE折叠,使点B落在长方形内点F处,且DF=6.
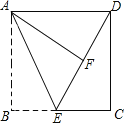
(1)试说明:△ADF是直角三角形;
(2)求BE的长.
【答案】(1)见解析;(2)BE=4.
【解析】
(1)由折叠的性质可知AF=AB=8,然后再依据勾股定理的逆定理可证明△ADF为直角三角形;
(2)由题意可证点E、D、F在一条直线上,设BE=x,则EF=x,DE=6+x,EC=10-x,在Rt△CED中,依据勾股定理列方程求解即可.
(1)将△ABE沿AE折叠,使点B落在长方形内点F处,
∴AF=AB=8,
∵AF2+DF2=62+82=100=102=AD2,
∴∠AFD=90°
∴△ADF是直角三角形
(2)∵折叠
∴BE=EF,∠B=∠AFE=90°
又∵∠AFD=90°
∴点D,F,E在一条直线上.
设BE=x,则EF=x,DE=6+x,EC=10-x,
在Rt△DCE中,∠C=90°,
∴CE2+CD2=DE2,
即(10-x)2+82=(6+x)2.
∴x=4.
∴BE=4.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
在平面直角坐标系中,已知点![]() ,点
,点![]() 是
是![]() 轴上的一个动点.
轴上的一个动点.

自主探究:
(1)点![]() 到
到![]() 轴的距离是_______,到原点的距离是 .
轴的距离是_______,到原点的距离是 .
(2)点![]() 关于
关于![]() 轴的对称点坐标为________,关于原点的对称点的坐标为 .
轴的对称点坐标为________,关于原点的对称点的坐标为 .
探索发现:
(3)当![]() 取何值时,
取何值时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=6,BC=8,若AC,BC边上的中线BE,AD 垂直相交于点O,则AB=( )

A. 5 B. 4![]() C. 3
C. 3![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点G为BC边的中点,点H在AF上,动点P以每秒2cm的速度沿图1的边运动,运动路径为G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图2,若AB=6cm,则下列结论正确的个数有( )
①图1中BC长4cm;
②图1中DE的长是6cm;
③图2中点M表示4秒时的y值为24cm2;
④图2中的点N表示12秒时y值为15cm2.

A.4 个B.3 个C.2 个D.1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
(1)若m=-3,求抛物线的解析式,并写出抛物线的对称轴;
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在抛物线对称轴左侧上有 一点E,使S△ACE=S△ACD,求E点的坐标;
(3) 如图2,设F(-1,-4),FG⊥y轴于G,在线段OG上是否存在点P,使 ∠OBP=∠FPG? 若存在,求m的取值范围;若不存在,请说明理由.
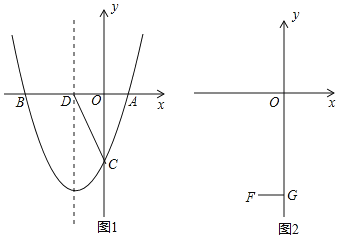
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南中国海是中国固有领海,我渔政船经常在此海域执勤巡察.一天我渔政船停在小岛A北偏西37°方向的B处,观察A岛周边海域.据测算,渔政船距A岛的距离AB长为10海里.此时位于A岛正西方向C处的我渔船遭到某国军舰的袭扰,船长发现在其北偏东50°的方向上有我方渔政船,便发出紧急求救信号.渔政船接警后,立即沿BC航线以每小时30海里的速度前往救助,问渔政船大约需多少分钟能到达渔船所在的C处?
![]() (参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)
(参考数据:sin37°≈0.60,cos37°≈0.80,sin50°≈0.77,cos50°≈0.64,sin53°≈0.80,cos53°≈0.60,sin40°≈0.64,cos40°≈0.77)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度是________ m.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com