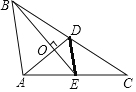
【题目】如图，在△ABC中，AC=6，BC=8，若AC，BC边上的中线BE,AD 垂直相交于点O，则AB=（ ）
A. 5 B. 4
C. 3
D. 2
【答案】D
【解析】
连接DE，根据三角形中线的定义可得E、D分别是AC、BC的中点，由此可得DE是△ABC的中位线，根据中位线的性质可得DE=
AB，接下来根据勾股定理结合图形即可解答.
解：∵BE、AD是△ABC的中线，AC=6，BC=8，
∴E、D分别是AC、BC的中点，BD=CD=4，AE=CE=3，
∴DE是△ABC的中位线，DE=AB，
∵BE⊥AD，
∴BO2+DO2=BD2=16……①，
AO2+EO2+AE2=9……②，
DO2+EO2=DE2=
AB2……③，
BO2+AO2=AB2……④，
∵①+②=BO2+DO2+AO2+EO2，③+④= BO2+DO2+AO2+EO2，
∴①+②=③+④，
∴16+9=AB2+AB2，
∴AB=2
.
故选D.
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点P的横坐标为x，纵坐标为2x，满足这样条件的点称为“关系点”.
(1)在点A(1,2)、B(2,1)、M(
，1)、N(1， 
)中，是“关系点”的为 ；
(2)⊙O的半径为1，若在⊙O上存在“关系点”P，求点P坐标；
(3)点C的坐标为(3，0)，若在⊙C上有且只有一个“关系点”P，且“关系点”P的横坐标满足-2≤x≤2.请直接写出⊙C的半径r的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列判断正确的是（ ）
A. “任意选择某一电视频道，它正在播放动画片”是必然事件
B. 某运动员投一次篮，投中的概率为0.8，则该运动员投5次篮，一定有4次投中
C. 任意抛掷一枚均匀的硬币，反面朝上的概率为
D. 布袋里有3个白球，1个黑球．任意取出1个球，恰好是黑球的概率是
查看答案和解析>>
科目：初中数学 来源： 题型：
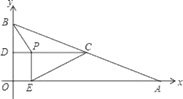
【题目】在平面直角坐标系中，已知点A、B的坐标分别为（10，0）、（0，4），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C以每秒1个单位匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线垂直时，点P运动的时间为_____秒．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在长方形ABCD中，AB=8，AD=10，点E为BC上一点，将△ABE沿AE折叠，使点B落在长方形内点F处，且DF=6．
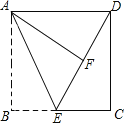
（1）试说明：△ADF是直角三角形；
（2）求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小聪和小明沿同一条路同时从学校出发到学校图书馆查阅资料，学校与图书馆的路程是
千米，小聪骑自行车，小明步行，当小聪从原路回到学校时，小明刚好到达图书馆，图中折线
和线段
分别表示两人离学校的路程
（千米）与所经过的时间
（分钟）之间的函数关系，请根据图象回答下列问题：
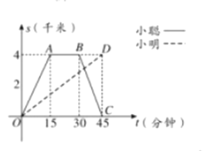
（1）小聪在图书馆查阅资料的时间为 分钟，小聪返回学校的速度为 千米/分钟；
（2）请你求出小明离开学校的路程（千米）与所经过的时间（分钟）之间的函数关系；
（3）求线段
的函数关系式；
（4）当小聪与小明迎面相遇时，他们离学校的路程是多少千米？
查看答案和解析>>
科目：初中数学 来源： 题型：
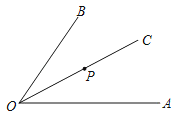
【题目】如图，∠AOB＝60°，OC平分∠AOB，P为射线OC上一点，如果射线OA上的点D，满足△OPD是等腰三角形，那么∠ODP的度数为（ ）
A.30°B.120°
C.30°或120°D.30°或75°或120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
