
【题目】如图,E,F分别是矩形ABCD的边AB,AD上的点,∠FEC=∠FCE=45°.
(1)求证:AF=CD.
(2)若AD=3,△EFC的面积为4,求线段BE的长.

【答案】(1)详见解析.(2)![]() .
.
【解析】
(1)由AAS证明△AEF≌△DFC,即可得出结论;
(2)由△EFC的面积求出EF=CF,由勾股定理求出EC,再由勾股定理求出BE即可.
(1)证明:∵在△CEF中,∠FEC=∠FCE=45°,
∴FE=FC,∠EFC=90°,
∴∠AFE+∠CFD=90°,
又∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠CFD+∠DCF=90°,
∴∠AFE=∠DCF,
在△AEF和△DFC中,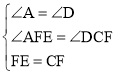 ,
,
∴△AEF≌△DFC(AAS)
∴AF=CD;
(2)解:由(1)得△CEF中,∠EFC=90°,FE=FC,△EFC的面积为4
∴![]()
∴![]() ,
,
在Rt△CEF中,![]() ,
,
又∵四边形ABCD是矩形,∴∠B=90°,AD=BC=3
∴在Rt△BEC中,BE2=CE2﹣BC2=16﹣32=7,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() .
.
(1)求证:它的图象与x轴必有两个不同的交点;
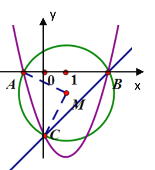
(2)这条抛物线与x轴交于两点A(x1,0),B(x2,O)(x1<x2),与y轴交于点C,且AB=4,⊙M过A,B,C三点,求扇形MAC的面积S;
(3)在(2)的条件下,抛物线上是否存在点P,PD⊥x轴于D,使△PBD被直线BC分成面积比为1:2的两部分?若存在,请求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )

A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点G.

求证:(1)DG⊥AG;
(2)AG+CG=AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
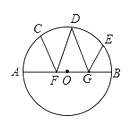
【题目】如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
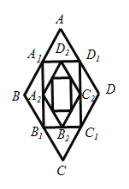
【题目】如图,菱形![]() 的边长为6,∠A=60°.取菱形各边中点
的边长为6,∠A=60°.取菱形各边中点![]() 并顺次连接这四个点,得到四边形
并顺次连接这四个点,得到四边形![]() ,再取四边形
,再取四边形![]() 各边中点
各边中点![]() ,顺次连接得到四边形
,顺次连接得到四边形![]() ……以此类推,则四边形
……以此类推,则四边形![]() 的面积是_______.
的面积是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的质地均匀转盘![]() 、
、![]() 都被分成了
都被分成了![]() 个全等的扇形,在每一扇形内均标有不同的自然数,如图所示.转动转盘
个全等的扇形,在每一扇形内均标有不同的自然数,如图所示.转动转盘![]() 、
、![]() ,两个转盘停止后观察两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向下方的扇形).
,两个转盘停止后观察两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向下方的扇形).
(1)小明同学转动转盘![]() ,小华同学转动转盘
,小华同学转动转盘![]() ,他们都转了
,他们都转了![]() 次,结果如下:
次,结果如下:
指针停靠的扇形内的数字 |
|
|
|
|
|
|
出现的次数 |
|
|
|
|
|
|
![]() 求出表中
求出表中![]() 的值.
的值.
![]() 计算
计算![]() 盘中“指针停靠的扇形内的数字为
盘中“指针停靠的扇形内的数字为![]() ”的频率;
”的频率;
(2)小明转动![]() 盘一次,指针停靠的扇形内的数字作为十位数字,小华转动
盘一次,指针停靠的扇形内的数字作为十位数字,小华转动![]() 盘一次,指针停靠的扇形内的数字作为个位数字,用列表或画树状图的方法求出“所得的两位数为
盘一次,指针停靠的扇形内的数字作为个位数字,用列表或画树状图的方法求出“所得的两位数为![]() 的倍数”(记为事件
的倍数”(记为事件![]() )的概率.
)的概率.
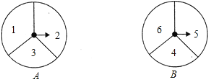
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com