
【题目】如图,在![]() 中,
中,![]() ,在同一平面内,将
,在同一平面内,将![]() 绕点
绕点![]() 旋转到
旋转到![]() 的位置,使得
的位置,使得![]() ,则
,则![]() ( )
( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
【题目】在探究平行线的判定——基本事实:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行时,老师布置了这样的任务:
请同学们分组在学案上(如图),用直尺和三角尺画出过点P与直线AB平行的直线PQ;并思考直尺和三角尺在画图过程中所起的作用.

小菲和小明所在的小组是这样做的:他们选取直尺和含有45°角的三角尺,用平移三角尺的画图方法画出AB的平行线PQ,并将实际画图过程抽象出平面几何图形(如图).

以下是小菲和小明所在小组关于直尺和三角尺作用的讨论:
①在画平行线的过程中,三角尺由初始位置靠着直尺平移到终止位置,实际上就是先画∠BMD=45°,再过点P画∠BMD=45°
②由初始位置的三角尺和终止位置的三角尺各边所在直线构成一个“三线八角图”,其中QP为截线
③初始位置的三角尺和终止位置的三角尺在“三线八角图”中构成一组同位角
④在画图过程中,直尺可以由直线CD代替
⑤在“三线八角图”中,因为AB和CD是截线,所以,可以下结论“两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行”
其中,正确的是( )
A.①②⑤B.①③④C.②④⑤D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点D在边BC上,DE⊥AB于E,DH⊥AC于H,且满足DE=DH,F为AE的中点,G为直线AC上一动点,满足DG=DF,若AE=4cm,则AG= _____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AM,CN分别是∠BAD和∠BCD的平分线,添加一个条件,仍无法判断四边形AMCN为菱形的是( )

A.AM=AN B.MN⊥AC
C.MN是∠AMC的平分线 D.∠BAD=120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,若平移点
,若平移点![]() 到点
到点![]() ,使以点
,使以点![]() 为顶点的四边形是菱形,则正确的平移方法是( )
为顶点的四边形是菱形,则正确的平移方法是( )

A. 向左平移(![]() )个单位,再向上平移1个单位
)个单位,再向上平移1个单位
B. 向左平移![]() 个单位,再向下平移1个单位
个单位,再向下平移1个单位
C. 向右平移![]() 个单位,再向上平移1个单位
个单位,再向上平移1个单位
D. 向右平移2个单位,再向上平移1个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=6,CD=8,E,F分别是边ABCD的中点, DH⊥BC于点H,连接EH,EC,EF,现有下列结论:①∠CDH=30°;②EF=4;③四边形EFCH是菱形;④S△EFC=3S△BEH.你认为结论正确的有___________.(填序号)
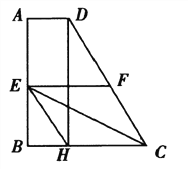
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在真角坐标系中,矩形0ABC的顶点A,C在坐标轴上,点B(4,2);过点D(0,3)和E(6,0)的直线分别与AB、BC交于点M、N.
(1)求直线DE的函数表达式和点M,N的坐标;
(2)若函数y=![]() (k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(k≠0,k为常数)经过点M,求该函数的表达式,并判定点N是否在该函数的图象上:
(3)求△OMN的面积S;
(4)若函教y=![]() (k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.
(k≠0,k为常数)的图象与△BMN没有交点,清楚直接写出k的取值范圈,不需解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com