
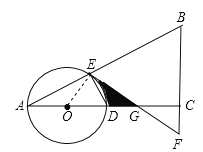
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,OA为半径的圆分别交AB,AC于点E,D,在BC的延长线上取点F,使得BF=EF,EF与AC交于点G.
(1)试判断直线EF与⊙O的位置关系,并说明理由;
(2)若OA=2,∠A=30°,求图中阴影部分的面积.

【答案】(1)EF是⊙O的切线,理由见解析;(2)![]() .
.
【解析】试题分析:(1)连接OE,根据等腰三角形的性质得到∠A=∠AEO,∠B=∠BEF,于是得到∠OEG=90°,即可得到结论;(2)由AD是⊙O的直径,得到∠AED=90°,根据三角形的内角和得到∠EOD=60°,求得∠EGO=30°,根据三角形和扇形的面积公式即可得到结论.
试题解析:(1)连接OE,
∵OA=OE,∴∠A=∠AEO,
∵BF=EF,∴∠B=∠BEF,
∵∠ACB=90°,∴∠A+∠B=90°,∴∠AEO+∠BEF=90°,
∴∠OEG=90°,∴EF是⊙O的切线;
(2)∵AD是⊙O的直径,∴∠AED=90°,
∵∠A=30°,∴∠EOD=60°,∴∠EGO=30°,
∵AO=2,∴OE=2,∴EG=2![]() ,
,
∴阴影部分的面积=![]() =
= ![]() .
.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
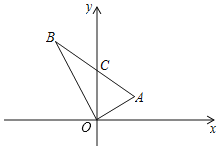
【题目】如图,在平面直角坐标系中,O为原点,点A(2,1),B(﹣2,4),直线AB与y轴交于点C.
(1)求点C的坐标;
(2)求证:△OAB是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角三角形的直角顶点重合,∠AOC=40°,求∠BOD 的度数.
结合图形,完成填空:
解法 1:
因为![]() ,
,![]()
所以![]()
![]()
因为![]()
![]()
所以![]()
![]()
![]()
所以![]()
![]()
解法2:
因为![]()
![]() ,
,![]()
![]() ,①
,①
所以![]() .②
.②
因为![]()
所以![]()
![]()
在上面①到②的推导过程中,理由依据是: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市要销售一种新上市的文具,进价为20元,试营销阶段发现:当销售单价是25元时,每天的销售量为250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)求销售单价为多少元时,该文具每天的销售利润最大,并求出最大的利润;
(2)经过试营销后,超市按(1)中单价销售,为了回馈广大顾客,同时提高该文具知名度,超市决定在1月1日当天开展降价促销活动,若每件文具降价2a%,则可多售出4a%,结果当天销售额为5670元,要使销量尽可能地大,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是直线![]() 外一点,在
外一点,在![]() 上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是:_________________________
上取两点A,B,连接AD,分别以点B,D为圆心,AD,AB的长为半径画弧,两弧交于点C,连接CD,BC,则四边形ABCD是平行四边形,理由是:_________________________
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板的两直角边所在直线分别与直线BC,CD交于点M,N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是__________________;
(2)如图2,若点O在正方形的中心(即两对角线的交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说理)

查看答案和解析>>
科目:初中数学 来源: 题型:
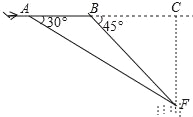
【题目】“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止),此时的俯角为30°.为了便于观察,飞机继续向前飞行了800m到达B点,此时测得点F的俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A,B,C在同一直线上),竖直高度CF约为多少米?(结果保留整数.参考数据:![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com