
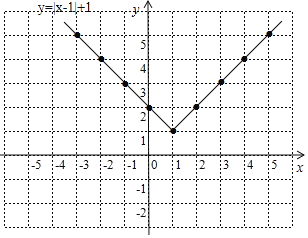
【题目】某校数学兴趣小组,对函数y=|x﹣1|+1的图象和性质进行了探究,探究过程如下:
(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | … |
其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
(3)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x=1的右侧,函数图象呈上升状态 | 当x>1时,y随x的增大而增大 |
① | 在直线x=1的左侧,函数图象呈下降状态 |
|
示例2 | 函数图象经过点(﹣3,5) | 当x=﹣3时,y=5 |
② | 函数图象的最低点是(1,1) |
|
(4)当2<y≤4时,x的取值范围为 .

【答案】(1)3;(2)详见解析;(3)详见解析;(4)﹣2≤x<0或2<x≤4.
【解析】
(1)把x=﹣1代入求出y的值即可;
(2)根据表中数据描点、连线即可得出函数的图象;
(3)①根据函数的图象直观得出结论,②函数的最低点,即函数y有最小值;
(4)根据函数图象,当2<y≤4时,对应的是两段图象,即自变量的取值范围有两部分,从图象中可以得出答案.
解:(1)把x=﹣1代入y=|x﹣1|+1得,m=y=3;
故答案为:3;
(2)画出的函数图象,如图所示:
(3)由函数图象可得:①当x<1时,y随x的增大而减小;
②当x=1时,y的最小值为1;
(4)根据图象可知:当2<y≤4时,相应x的取值范围为﹣2≤x<0或2<x≤4.
故答案为:﹣2≤x<0或2<x≤4.


科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4)
(1)画出△ABC先向左平移1个单位,再向下平移4个单位得到的△A1B1C1,写出点A1的坐标____________
(2)画出△A1B1C1绕原点O顺时针旋转90°,得到△A2B2C2,写出点A2的坐标_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①倒数等于本身的数是±1;②互为相反数的两个非零数的商为﹣1;③如果两个数的绝对值相等,那么这两个数相等;④有理数可以分为正有理数和负有理数;⑤单项式﹣![]() 的系数是﹣
的系数是﹣![]() ,次数是6;⑥多项式3πa3+4a2﹣8是三次三项式,其中正确的个数是( )
,次数是6;⑥多项式3πa3+4a2﹣8是三次三项式,其中正确的个数是( )
A. 2 个B. 3 个C. 4 个D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数就为“奇巧数,如![]() ,因此
,因此![]() 这三个数都是奇巧数。
这三个数都是奇巧数。
![]() 都是奇巧数吗?为什么?
都是奇巧数吗?为什么?
![]() 设这两个连续偶数为
设这两个连续偶数为![]() (其中
(其中![]() 为正整数),由这两个连续偶数构造的奇巧数是
为正整数),由这两个连续偶数构造的奇巧数是![]() 的倍数吗?为什么?
的倍数吗?为什么?
![]() 研究发现:任意两个连续“奇巧数”之差是同一个数,请给出验证。
研究发现:任意两个连续“奇巧数”之差是同一个数,请给出验证。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系,若△AOB绕点O逆时针旋转90后,得到△A1OB1(A和A1是对应点)
(1)写出点A1,B1的坐标 ;
(2)求旋转过程中边OB扫过的面积(结果保留π);

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com