
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是弧EB的中点,则下列结论:
①OC∥AE;②EC=BC;③∠DAE=∠ABE;④AC⊥OE,其中正确的有( )
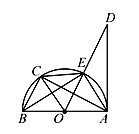
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产一件A种产品用甲种原料9千克,乙种原料3千克,可获利700元;生产一件B种产品用甲种原料4千克,乙种原料10千克,可获利1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;
(2)设生产A、B两种产品总利润为y元,其中一种产品生产件数为x件,试写出y与x之间的函数关系式,并利用函数的性质说明那种方案获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学老师在课堂上展示一矩形纸片,如图,在矩形ABCD中,AB=6cm,BC=8cm.他要将此矩形做一个梯形教具,现进行如下操作:
先将矩形ABCD的点D折叠到对角线AC上的点F处,折痕为CE,再将折叠的部分裁掉;

问:(1)所裁部分DE的长;
(2)所裁成的梯形ABCE的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,⊙O过BC的中点D,且DE垂直AC于E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若AB=13,BC=10,求DE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是平行四边形,对角线AC平分∠DAB,AC与BD相交于点O,DE⊥AB于E点.(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求DE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABO中,AB⊥OB,OB=![]() ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1的坐标为

A.(﹣1,![]() ) B.(﹣1,
) B.(﹣1,![]() )或(﹣2,0) C.(
)或(﹣2,0) C.(![]() ,﹣1)或(0,﹣2) D.(
,﹣1)或(0,﹣2) D.(![]() ,﹣1)
,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com