
【题目】四边形ABCD是平行四边形,对角线AC平分∠DAB,AC与BD相交于点O,DE⊥AB于E点.(1)求证:四边形ABCD是菱形;
(2)若AC=8,BD=6,求DE的长度.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)由对角线AC平分∠DAB证明平行四边形ABCD的邻边AB=BC即可证明四边形ABCD是菱形;
(2)根据菱形的性质求得AB的长,再根据菱形面积的两种表示方式即可求解.
试题解析:(1)∵四边形ABCD是平行四边形,∴AD//BC,∴∠DAC=∠BCA,
∵AC平分∠DAB,∴∠DAC=∠BAC,∴∠BCA=∠BAC,∴AB=BC,
∵四边形ABCD是平行四边形,∴平行四边形ABCD为菱形;
(2)在菱形ABCD中,AC=8,BD=6,∴AO=4,BO=3,AC⊥BD,∴AB=5,
2S△ABD=AB·DE=![]() AC·BD,∴5DE=
AC·BD,∴5DE=![]() x8x6,∴DE=
x8x6,∴DE=![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场销售一批小家电,平均每天可售出20台,每台盈利40元.为了去库存,商场决定采取适当的降价措施.经调查发现,在一定范围内,小家电的单价每降5元,商场平均每天可多售出10台.
(1)若将这批小家电的单价降低x元,则每天的销售量是______台(用含x的代数式表示);
(2)如果商场通过销售这批小家电每天要盈利1250元,那么单价应降多少元?
(3)若这批小家电的单价有三种降价方式:降价10元、降价20元、降价30元,如果你是商场经理,你准备采取哪种降价方式?说说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )

A.直角三角形的面积
B.最大正方形的面积
C.较小两个正方形重叠部分的面积
D.最大正方形与直角三角形的面积和
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
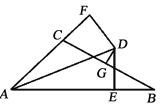
【题目】如图,∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=11,AC=5,则BE=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的运货情况如下表:
第一次 | 第二次 | |
甲种货车的辆数 | 2辆 | 5辆 |
乙种货车的辆数 | 3辆 | 6辆 |
累计运货重量 | 14吨 | 32吨 |
(1)分别求甲乙两种货车每辆载重多少吨?
(2)现租用该公司3辆甲种货车和5辆乙种货车刚好一次运完这批货物,如果按每吨付运费120元计算,货主应付运费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
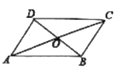
(1)求证:四边形ABCD是平行四边形
(2)若AC⊥BD,且AB=4,则四边形ABCD的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小兰:“小红,你上周买的笔和笔记本的价格是多少啊?”小红:“哦,…,我忘了!只记得先后买了两次,第一次买了 5 支笔和 10 本笔记本共花了 42 元钱,第二次买了 10 文笔和 5 本笔记本共花了 30 元钱.”请根据小红与小兰的对话,求得小红所买的笔和笔 记本的价格分别是( )
A.0.8 元/支,2.6 元/本B.0.8 元/支,3.6 元/本
C.1.2 元/支,2.6 元/本D.1.2 元/支,3.6 元/本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】珍珍与环环两人一起做游戏,游戏规则如下:每人从1,2,3,4,5,6,7,8中任意选择一个数字,然后两人各转动一次如图所示的转盘(转盘被分为面积相等的四个扇形),两人转出的数字之和等于谁事先选择的数,谁就获胜;若两人转出的数字之和不等于她们各自选择的数,就再做一次上述游戏,直到决出胜负.若环环事先选择的数是5,用列表法或画树状图的方法,求她获胜的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com