
【题目】一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )
A.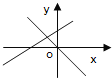 B.
B.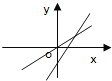 C.
C.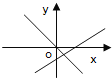 D.
D.
【答案】C
【解析】
由于m、n的符号不确定,故应先讨论m、n的符号,再根据一次函数的性质进行选择.
解:(1)当m>0,n>0时,mn>0, 一次函数y=mx+n的图象一、二、三象限, 正比例函数y=mnx的图象过一、三象限,无符合项;
(2)当m>0,n<0时,mn<0, 一次函数y=mx+n的图象一、三、四象限, 正比例函数y=mnx的图象过二、四象限,C选项符合;
(3)当m<0,n<0时,mn>0, 一次函数y=mx+n的图象二、三、四象限, 正比例函数y=mnx的图象过一、三象限,无符合项;
(4)当m<0,n>0时,mn<0, 一次函数y=mx+n的图象一、二、四象限, 正比例函数y=mnx的图象过二、四象限,无符合项.
故选:C.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗?
小敏在思考问题时,有如下思路:连接AC.

结合小敏的思路作答:
(1)若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;
(2)如图2,在(1)的条件下,若连接AC,BD.
①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组,对函数y=|x﹣1|+1的图象和性质进行了探究,探究过程如下:
(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | … |
其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
(3)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x=1的右侧,函数图象呈上升状态 | 当x>1时,y随x的增大而增大 |
① | 在直线x=1的左侧,函数图象呈下降状态 |
|
示例2 | 函数图象经过点(﹣3,5) | 当x=﹣3时,y=5 |
② | 函数图象的最低点是(1,1) |
|
(4)当2<y≤4时,x的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于
于![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)当![]() 为
为![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若![]() 为
为![]() 中点,则当
中点,则当![]() ________时,四边形
________时,四边形![]() 是正方形
是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
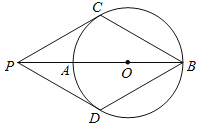
【题目】如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙上一点,连接PD.已知PC=PD=BC.下列结论:
(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 A、B 在数轴上分别表示有理数 a、b.
(1)对照数轴,填写下表:

(2)若 A、B 两点间的距离记为 d,试问 d 和 a、b(a<b)有何数量关系?数学式子表示.
(3)求所有到数 5 和-5 的距离之和为 10 的整数的和,列式计算.
(4)若点 C 表示的数为 x,当点 C 在什么位置时,|x+1|+|x﹣2|取得的值最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
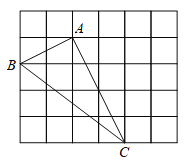
【题目】如图,在由边长为1的小正方形组成的网格中,![]() 的三个顶点均在格点上,请解答:
的三个顶点均在格点上,请解答:
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)在网格图中画出AD//BC,且AD=BC;
(3)连接CD,若E为BC中点,F为AD中点,四边形AECF是什么特殊的四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是AD边的中点.
(1)用直尺和圆规作⊙O,使⊙O 经过B、C、E三点;(要求:尺规作图,保留作图痕迹,不写作法);
(2)若正方形的边长为4,求(1)中所作⊙O的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com