
【题目】如图是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O.
(1)若∠OAB=25°,求∠APB的度数;
(2)若∠OAB=n°,请直接写出∠APB的度数.

【答案】(1)∠APB=50°;(2)∠APB=2n°.
【解析】
(1)连接OB,由AO=OB得,∠OAB=∠OBA=25°,∠AOB=180°-2∠BAB=130°;因为PA、PB分别相切于点A、B,则∠OAP=∠OBP=90°,所以∠APB=180°-∠AOB=50°.
(2)同(1)的解题思路一致,利用三角形内角和与四边形内角和推出结果.
解:(1)连接OB,
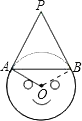
∵PA、PB切⊙O于A、B,
∴OA⊥PA,OP⊥AB,
∴∠OAP+∠OBP=180°,
∴∠APB+∠AOB=180°;
∵OA=OB,
∴∠OAB=∠OBA=25°,
∴∠AOB=130°,
∴∠APB=50°;
(2)连接OB,
∵PA、PB切⊙O于A、B,
∴OA⊥PA,OP⊥AB,
∴∠OAP+∠OBP=180°,
∴∠APB+∠AOB=180°;
∵OA=OB,
∴∠OAB=∠OBA=n°,
∴∠AOB=180°- 2n°,
∴∠APB=2n°.


科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
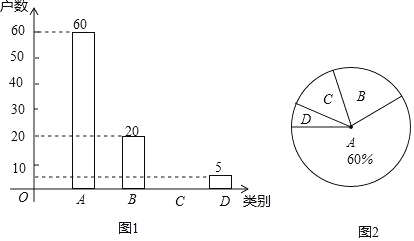
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年世界杯足球赛的“大力神杯”系列纪念品是中国制造.某商店用10000元购进一批“大力神杯”钥匙扣进行销售,很快销售一空.然后商店又用24000元购进这种钥匙扣,所购数量是第一批购进数量的2倍,但每个钥匙扣的价格比第一批的价格多了2元.
(1)该商店第一批购进的钥匙扣单价是多少元?
(2)若该商店第一、二批购进的钥匙扣都按相同的标价出售,并且全部售完,要使利润不低于20%,则每个钥匙扣的标价至少是多少元?
(3)在销售第二批钥匙扣时发现,若以每个15元价格出售,可全部售完.每涨价1元,销售量减少100件,剩余钥匙扣以每个10元价格全部售出.设该商店在销售第二批钥匙扣所获利润为P元,销售单价为m元,求P与m的函数关系式,并求出利润P最大时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个函数y=2x+3与二次函数y=ax2+bx+c的图象交于A(m,5)和B(3,n)两点,且点B是抛物线的顶点.
(1)求二次函数的解析式;
(2)请在给出的平面直角坐标系中画出一次函数和二次函数的简图(无需列表),并根据简图写出:
当x满足 时,两个函数的值都随x的增大而增大?
当x满足 时,二次函数的函数值大于零?
当x满足 是,二次函数的值大于一次函数的值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一个三角形一条边上的高等于这条边长的一半,则称该三角形为“半高”三角形,这条高称为“半高”.

(1)如图1,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 求证:
求证: ![]() 是“半高”三角形;
是“半高”三角形;
(2)如图2,![]() 是“半高”三角形,且
是“半高”三角形,且![]() 边上的高是“半高”,点
边上的高是“半高”,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
①请探究![]() ,
,![]() ,
,![]() 之间的等量关系,并说明理由;
之间的等量关系,并说明理由;
②若![]() 的面积等于16,求
的面积等于16,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:![]() 的值为 :
的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2![]() ,则BC= .
,则BC= .

查看答案和解析>>
科目:初中数学 来源: 题型:
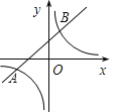
【题目】如图,已知一次函数与反比例函数的图象交于点A(-4,-1)和B(a,2).
(1)求反比例函数的解析式和点B的坐标.
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
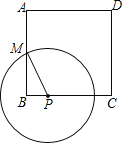
【题目】如图,正方形ABCD的边长为6,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com