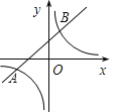
【题目】如图，已知一次函数与反比例函数的图象交于点A(-4，-1)和B(a，2)．
（1）求反比例函数的解析式和点B的坐标．
（2）根据图象回答，当x在什么范围内时，一次函数的值大于反比例函数的值？
【答案】（1）y=
，B(2，2)；（2）当x＞2或-4＜x＜0时，一次函数的值大于反比例函数的值
【解析】
（1）根据反比例函数图象经过点A（-4，-1），可以求得反比例函数的解析式，再根据点B在反比例函数图象上，即可求得点B的坐标；
（2）根据函数图象可以直接写出当x在什么范围内时，一次函数的值大于反比例函数的值．
解：（1）设反比例函数的解析式为y=
，
∵反比例函数图象经过点A（-4，-1），
∴-1=
，解得k=4，
∴反比例函数的解析式为y=
，
∵B（a，2）在y=的图象上，
∴2=
，解得a=2，
∴点B的坐标为B（2，2）；
（2）由图象得，交点A（-4，-1），B（2，2），
当x＞2或-4＜x＜0时，y轴方向上直线在曲线的上方即一次函数的值大于反比例函数的值．
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】使用家用燃气灶烧开同一壶水所需的燃气量
（单位：
）与旋钮的旋转角度
（单位：度）（
）近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度与燃气量的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是不倒翁的正视图，不倒翁的圆形脸恰好与帽子边沿PA、PB分别相切于点A、B，不倒翁的鼻尖正好是圆心O．
（1）若∠OAB=25°，求∠APB的度数；
（2）若∠OAB=n°，请直接写出∠APB的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，
，E为边BC上一点，且EC=AD，连接AC.
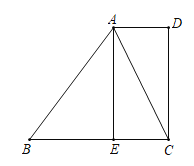
（1）求证：四边形AECD是矩形；
（2）若AC平分∠DAB，AB=5，EC=2，求AE的长，
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩用下面的折线统计图表示：（甲为实线，乙为虚线）
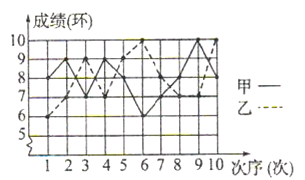
（1）依据折线统计图，得到下面的表格：
射击次序（次） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩（环） | 8 | 9 | 7 | 9 | 8 | 6 | 7 |
| 10 | 8 |
乙的成绩（环） | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 |
| 10 |
其中
________，
________；
（2）甲成绩的众数是________环，乙成绩的中位数是________环；
（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？
（4）该校射击队要参加市组织的射击比赛，已预选出2名男同学和2名女同学，现要从这4名同学中任意选取2名同学参加比赛，请用列表或画树状图法，求出恰好选到1男1女的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，BC∥OA，BC=3，OA=6，AB=3
（1）直接写出点B的坐标
（2）已知D.E分别为线段OC.OB上的点，OD=5，OE=2BE，直线DE交x轴于点F，求直线DE的解析式
（3）在（2）的条件下，点M是直线DE上的一点，在x轴上方是否存在另一个点N，使以O.D.M.N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由。
查看答案和解析>>
科目：初中数学 来源： 题型：
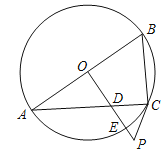
【题目】如图，已知AB是⊙O的直径，过O点作OP⊥AB，交弦AC于点D，交⊙O于点E，且使∠PCA=∠ABC．
(1)求证：PC是⊙O的切线；
(2)若∠P=60°，PC=2，求PE的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
