
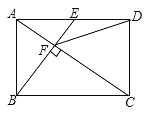
【题目】如图,在矩形![]() 中,
中,![]() 是
是![]() 边的中点,
边的中点,![]() 于点
于点![]() ,连接
,连接![]() .下列结论不正确的是( )
.下列结论不正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由于AE∥BC,则根据相似三角形的判定可对A选项进行判断;利用相似三角形的性质可对B选项进行判断;作DH⊥AC于H,如图,证明EF∥DH,则根据平行线分线段成比例定理得到AF=FH,则可证明DH垂直平分CF,从而可对C选项进行判断;设AF=x,则FH=CH=x,利用摄影定理可计算出DH=![]() ,然后根据正切的定义可对D进行判断.
,然后根据正切的定义可对D进行判断.
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,∠ABC=90°
∵E是AD边的中点,
∴BC=AD=2AE,
∵AE∥BC,
∴∠ACB=∠FAE
∵![]()
∴∠AFE=90°
∴∠AFE=∠ABC=90°
∴△AEF∽△CAB,所以A选项的结论正确;
∴![]() ,
,
∴CF=2AF,所以B选项的结论正确;
作DH⊥AC于H,如图,
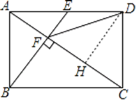
∵BE⊥AC,
∴EF∥DH,
![]() ,
,
即AF=FH,
而CF=2AF,
∴CH=FH,
∴DH垂直平分CF,
∴DF=DC,所以C选项的结论正确;
∵四边形ABCD是矩形,
∴∠ADC=90°,
∴∠ADH+∠CDH=90°,
∵DH⊥AC,
∴∠AHD=∠CHD=90°
∴∠HAD+∠HAD=90°,
∴∠HAD=∠CDH,
∴△AHD∽△DHC
∴![]()
设AF=x,则FH=CH=x,
∴DH2=AHCH=2xx,
∴DH=![]()
在Rt△AHD中,![]() ,
,
即![]() ,所以D选项的结论错误.
,所以D选项的结论错误.
故选:D.


 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠C=90°,AC=3,BC=4,O是BC的中点,到点O的距离等于![]() BC的所有点组成的图形记为G,图形G与AB交于点D.
BC的所有点组成的图形记为G,图形G与AB交于点D.

(1)补全图形并求线段AD的长;
(2)点E是线段AC上的一点,当点E在什么位置时,直线ED与 图形G有且只有一个交点?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x﹣3)2+![]() 过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切.正确的结论是( )
过点C(0,4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:①抛物线的对称轴是直线x=3;②点C在⊙D外;③在抛物线上存在一点E,能使四边形ADEC为平行四边形;④直线CM与⊙D相切.正确的结论是( )
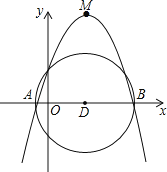
A.①③B.①④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
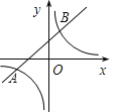
【题目】如图,已知一次函数与反比例函数的图象交于点A(-4,-1)和B(a,2).
(1)求反比例函数的解析式和点B的坐标.
(2)根据图象回答,当x在什么范围内时,一次函数的值大于反比例函数的值?
查看答案和解析>>
科目:初中数学 来源: 题型:
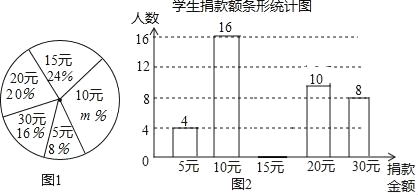
【题目】某中学为了帮助贫困学生读书,由校团委向全校2400名学生发起了“脱贫攻坚我在行”爱心捐款活动,为了解捐款情况,校团委随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图1和图2,请根据相关信息,解答下列问题:
(1)本次接受随机调查的学生人数为 ,图①中m的值是 ;
(2)请补全条形统计图;
(3)求本次调查获取的样本数据的众数和中位数;
(4)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】远承中学为了了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取了本校部分学生进行问卷调查(必选且只选一类节目),将调查结果进行整理后,绘制了如下不完整的条形统计图和扇形统计图,其中喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的3倍还多1人.
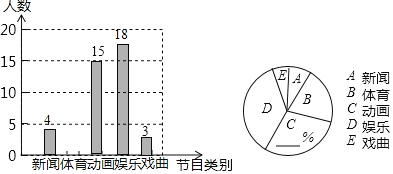
请根据所给信息解答下列问题:
(1)求本次抽取的学生人数;
(2)补全条形图,在扇形统计图中的横线上填上正确的数值;
(3)该校有5000名学生,请你估计该校喜爱娱乐节目的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com