
【题目】有一项工程,乙队单独完成所需的时间是甲队单独完成所需时间的2倍,若两队合作4天后,剩下的工作甲单独做还需要6天完成.
(1)求甲、乙两队单独完成这项工程各需多少天;
(2)若甲队每天的报酬是1万元,乙队每天的报酬是0.3万元,要使完成这项工程时的总报酬不超过9.6万元,甲队最多可以工作多少天?
【答案】(1) 甲队单独完成这项工程需要12天,乙队单独完成这项工程需要24天;(2) 甲队最多可以工作6天.
【解析】
(1)设甲队单独完成这项工程需要x天,则乙队单独完成这项工程需要2x天,根据甲队完成的部分+乙队完成的部分=整项工程(单位1),即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设甲队工作m天,则乙队工作![]() 天,根据总报酬=每天的报酬×工作时间结合总报酬不超过9.6万元,即可得出关于m的一元一次不等式,解之取其中最大值即可得出结论.
天,根据总报酬=每天的报酬×工作时间结合总报酬不超过9.6万元,即可得出关于m的一元一次不等式,解之取其中最大值即可得出结论.
(1)设甲队单独完成这项工程需要x天,则乙队单独完成这项工程需要2x天,
依题意,得:![]() =1,
=1,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴2x=24.
答:甲队单独完成这项工程需要12天,乙队单独完成这项工程需要24天.
(2)设甲队工作m天,则乙队工作![]() 天,
天,
依题意,得:m+0.3×![]() ≤9.6,
≤9.6,
整理,得:0.4m≤2.4,
解得:m≤6.
答:甲队最多可以工作6天.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】定义:若一个三角形一条边上的高等于这条边长的一半,则称该三角形为“半高”三角形,这条高称为“半高”.

(1)如图1,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 求证:
求证: ![]() 是“半高”三角形;
是“半高”三角形;
(2)如图2,![]() 是“半高”三角形,且
是“半高”三角形,且![]() 边上的高是“半高”,点
边上的高是“半高”,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
①请探究![]() ,
,![]() ,
,![]() 之间的等量关系,并说明理由;
之间的等量关系,并说明理由;
②若![]() 的面积等于16,求
的面积等于16,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】画图题:
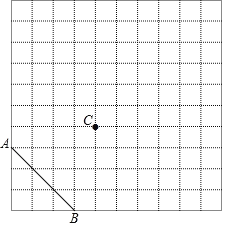
(1)在如图所示的方格纸中,经过线段AB外一点C,不用量角器与三角尺,仅用直尺,画线段AB的垂线CE和平行线CH.
(2)判断CE、CH的位置关系是 .
(3)连接AC和BC,若小正方形的边长为a,求三角形ABC的面积.(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
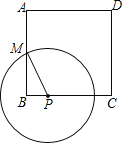
【题目】如图,正方形ABCD的边长为6,M是AB的中点,P是BC边上的动点,连结PM,以点P为圆心,PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时,BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为![]() 的等边
的等边![]() 和边长为
和边长为![]() 的等边
的等边![]() ,它们的边
,它们的边![]() ,
,![]() 位于同一条直线
位于同一条直线![]() 上,开始时,点
上,开始时,点![]() 与点
与点![]() 重合,
重合,![]() 固定不动,然后把
固定不动,然后把![]() 自左向右沿直线
自左向右沿直线![]() 平移,移出
平移,移出![]() 外(点
外(点![]() 与点
与点![]() 重合)停止,设
重合)停止,设![]() 平移的距离为
平移的距离为![]() ,两个三角形重合部分的面积为
,两个三角形重合部分的面积为![]() ,则
,则![]() 关于
关于![]() 的函数图象是( )
的函数图象是( )
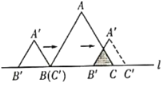
A.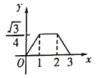 B.
B.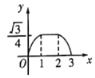 C.
C.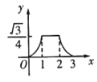 D.
D.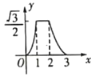
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=BC=5,AC=6.△ECD是△ABC沿BC方向平移得到的,连接AE.AC和BE相交于点O.
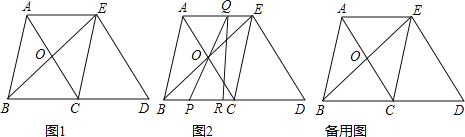
(1)判断四边形ABCE是怎样的四边形,说明理由;
(2)如图2,P是线段BC上一动点(图2),(不与点B、C重合),连接PO并延长交线段AE于点Q,QR⊥BD,垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化.若变化,请说明理由;若不变,求出四边形PQED的面积;
②当线段PB的长为何值时,△PQR与△BOC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AB为直径的⊙O与边AC相交于点D,BC是⊙O的切线,E为BC的中点,连接BD、DE.
(1)求DE是⊙O的切线;
(2)设△CDE的面积为S1,四边形ABED的面积为S2,若S2=5S1,求tan∠BAC的值;
(3)在(2)的条件下,连接AE,若⊙O的半径为2,求AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com