
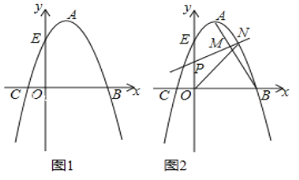
【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
【答案】(1)y=﹣x2+2x+3;(2)存在,G(1,0);(3)2.
【解析】
(1)根据顶点式可求得抛物线的表达式;
(2)根据轴对称的最短路径问题,作E关于对称轴的对称点E′,连接E′F交对称轴于G,此时EG+FG的值最小,先求E′F的解析式,它与对称轴的交点就是所求的点G;
(3)如图2,先利用待定系数法求AB的解析式,过N作NH⊥x轴于H,交AB于Q,设N(m,﹣m2+2m+3),则Q(m,﹣2m+6)(1<m<3),表示NQ=﹣m2+4m﹣3,证明△QMN∽△ADB,列比例式可得MN的表达式,根据配方法可得当m=2时,MN有最大值,证明△NGP∽△ADB,同理得PG的长,从而得OP的长,根据三角形的面积公式可得结论,并将m=2代入计算即可.
(1)设抛物线的表达式为:y=a(x﹣1)2+4,
把(0,3)代入得:3=a(0﹣1)2+4,
a=﹣1,
∴抛物线的表达式为:y=﹣(x﹣1)2+4=﹣x2+2x+3;
(2)存在,如图1,作E关于对称轴的对称点E',连接E'F交对称轴于G,此时EG+FG的值最小.
∵E(0,3),∴E'(2,3),
设EF的解析式为y=k′x+b′,
把F(0,﹣3),E'(2,3)分别代入,得![]() ,解得
,解得![]() ,
,
所以E'F的解析式为:y=3x﹣3,
当x=1时,y=3×1﹣3=0,∴G(1,0);
(3)如图2.
设AB的解析式为y=k″x+b″,
把A(1,4),B(3,0)分别代入,得![]() ,解得
,解得![]() ,
,
所以AB的解析式为:y=﹣2x+6,
过N作NH⊥x轴于H,交AB于Q,
设N(m,﹣m2+2m+3),则Q(m,﹣2m+6),(1<m<3),
∴NQ=(﹣m2+2m+3)﹣(﹣2m+6)=﹣m2+4m﹣3,
∵AD∥NH,∴∠DAB=∠NQM,
∵∠ADB=∠QMN=90°,∴△QMN∽△ADB,
∴![]() ,∴
,∴![]() ,
,
∴MN![]() (m﹣2)2
(m﹣2)2![]()
![]() 0,
0,
∴当m=2时,MN有最大值;
过N作NG⊥y轴于G,
∵∠GPN=∠ABD,∠NGP=∠ADB=90°,∴△NGP∽△ADB,
∴![]() ,∴PG
,∴PG![]() NG
NG![]() m,
m,
∴OP=OG﹣PG=﹣m2+2m+3![]() m=﹣m2
m=﹣m2![]() m+3,
m+3,
∴S△PON![]() OPGN
OPGN![]() (﹣m2
(﹣m2![]() m+3)m,
m+3)m,
当m=2时,S△PON![]() 2(﹣4+3+3)=2.
2(﹣4+3+3)=2.


科目:初中数学 来源: 题型:
【题目】如图,在过直线AB外一点P作直线AB的平行线时,可以按如下步骤进行:①在直线AB上任取两点C,D;②分别以点P,D为圆心,CD与PC为半径画弧,两弧交于点E;③作直线PE,则PE∥AB.在上面作图过程中,PE∥AB的依据是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动画片《小猪佩奇》分靡全球,受到孩子们的喜爱.现有4张《小猪佩奇》角色卡片,分别是A佩奇,B乔治,C佩奇妈妈,D佩奇爸爸(四张卡片除字母和内容外,其余完全相同).姐弟两人做游戏,他们将这四张卡片混在一起,背面朝上放好.
(1)姐姐从中随机抽取一张卡片,恰好抽到A佩奇的概率为 ;
(2)若两人分别随机抽取一张卡片(不放回),请用列表或画树状图的分方法求出恰好姐姐抽到A佩奇弟弟抽到B乔治的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
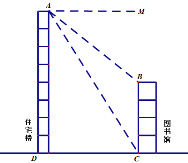
【题目】如图,小玲家在某24层楼的顶楼,对面新建了一幢28米高的图书馆,小玲在楼顶![]() 处看图书馆楼顶
处看图书馆楼顶![]() 处和楼底
处和楼底![]() 处的俯角分别是
处的俯角分别是![]() ,则两楼之间的距离是__________米.
,则两楼之间的距离是__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
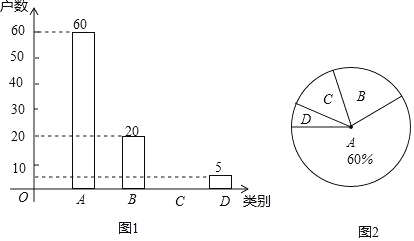
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)数轴上有A、B两点,若A点对应的数是﹣2,且A、B两点间的距离为3,则点B对应的数是________;
(2)已知线段AB=12cm,直线AB上有一点C,且BC=4cm,M是AC的中点,AM的长为________;
(3)已知∠AOB=3∠BOC,∠BOC=30°,则∠AOC=________;
(4)已知等腰三角形两边长为17、8,求三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(探索发现)
如图1,在正方形ABCD中,点M,N分别是边BC,CD上的点,∠MAN=45°,若将△DAN绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为8,则正方形ABCD的边长为 .
(2)(类比延伸)
如图2,在四边形ABCD中,AB=AD,∠BAD=120°,∠B+∠D=180°,点M,N分别在边BC,CD上的点,∠MAN=60°,请判断线段BM,DN,MN之间的数量关系,并说明理由.
(3)(拓展应用)
如图3,在四边形ABCD中,AB=AD=2,∠ADC=120°,点M,N分别在边BC,CD上,连接AM,MN,AN,△ABM是等边三角形,AM⊥AD于点A,∠DAN=15°,请直接写出△CMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
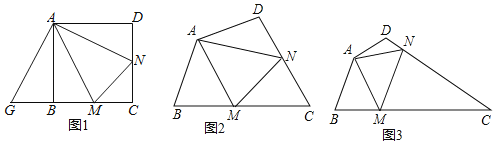
【题目】定义:若一个三角形一条边上的高等于这条边长的一半,则称该三角形为“半高”三角形,这条高称为“半高”.

(1)如图1,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() 求证:
求证: ![]() 是“半高”三角形;
是“半高”三角形;
(2)如图2,![]() 是“半高”三角形,且
是“半高”三角形,且![]() 边上的高是“半高”,点
边上的高是“半高”,点![]() 在
在![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .
.
①请探究![]() ,
,![]() ,
,![]() 之间的等量关系,并说明理由;
之间的等量关系,并说明理由;
②若![]() 的面积等于16,求
的面积等于16,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com