
【题目】(1)(探索发现)
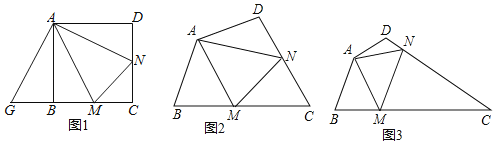
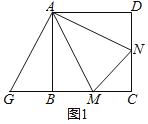
如图1,在正方形ABCD中,点M,N分别是边BC,CD上的点,∠MAN=45°,若将△DAN绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为8,则正方形ABCD的边长为 .
(2)(类比延伸)
如图2,在四边形ABCD中,AB=AD,∠BAD=120°,∠B+∠D=180°,点M,N分别在边BC,CD上的点,∠MAN=60°,请判断线段BM,DN,MN之间的数量关系,并说明理由.
(3)(拓展应用)
如图3,在四边形ABCD中,AB=AD=2,∠ADC=120°,点M,N分别在边BC,CD上,连接AM,MN,AN,△ABM是等边三角形,AM⊥AD于点A,∠DAN=15°,请直接写出△CMN的周长.
【答案】(1)4;(2)MN=NM+DN,理由见解析;(3)6+4![]()
【解析】
(1)求出MN=BM+DN,证明△MNC的周长=BC+CD即可解决问题;
(2)延长CB至E,使BE=DN,连接AE,首先证明△ABE≌△ADN,然后证明△MAN≌△MAE,根据全等三角形的性质可得结论;
(3)如图3,延长BA,CD交于G,解30度直角三角形求出DG和AG,进而得到BC和CD,然后根据(2)中结论计算即可.
解:(1)如图1中,∵△MAN≌△MAG,
∴MN=GM,
∵DN=BG,GM=BG+BM,
∴MN=BM+DN,
∵△CMN的周长为:MN+CM+CN=8,
∴BM+CM+CN+DN=8,
∴BC+CD=8,
∴BC=CD=4,
故答案为4;
(2)结论:MN=NM+DN.
理由:如图2中,延长CB至E,使BE=DN,连接AE,
∵∠ABC+∠D=180°,∠ABC+∠ABE=180°,
∴∠D=∠ABE,
在△ABE和△ADN中,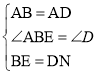 ,
,
∴△ABE≌△ADN(SAS),
∴AN=AE,∠DAN=∠BAE,
∵∠BAD=2∠MAN,
∴∠DAN+∠BAM=∠MAN,
∴∠MAN=∠EAM,
在△MAN和△MAE中,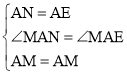 ,
,
∴△MAN≌△MAE(SAS),
∴MN=EM=BE+BM=BM+DN;
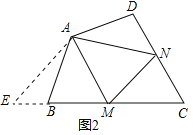
(3)如图3,延长BA,CD交于G,
∵∠BAM=60°,∠MAD=90°,
∴∠BAD=150°,
∴∠GAD=30°,
∵AD=2,
∴DG=1,AG=![]() ,
,
∵∠DAN=15°,
∴∠GAN=45°,
∴AG=GN=![]() ,
,
∴BG=2+![]() ,
,
∴BC=2BG=4+2![]() ,CG=
,CG=![]() BG=2
BG=2![]() +3,
+3,
∴CD=CG﹣DG=2![]() +2,
+2,
由(2)得,MN=BM+DN,
∴△CMN的周长=CM+CN+MN=CN+DN+CM+BM=BC+CD=4+2![]() +2
+2![]() +2=6+4
+2=6+4![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以每小时40海里的速度在海面上航行,当该轮船行驶到B处时,发现灯塔C在它的东北方向,轮船继续向北航行,30分钟后到达A处,此时发现灯塔C在它的北偏东75°方向上,求此时轮船与灯塔C的距离.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
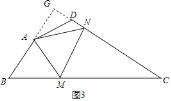
【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
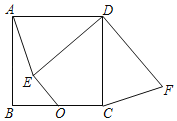
【题目】如图,正方形ABCD中,AB=2![]() ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加学校组织的智力竞答活动,竞赛中有两道单选题完全不会.这两道单选题各有A.B.C三个选项,第一道单选答案是B.第二道单选答案是C.最终两道题小明随机各写了一个答案
(1)小明答对第一道题的概率是 .
(2)请用树状图或者列表求出小明两道题都答对的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使用家用燃气灶烧开同一壶水所需的燃气量![]() (单位:
(单位:![]() )与旋钮的旋转角度
)与旋钮的旋转角度![]() (单位:度)(
(单位:度)(![]() )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度
)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度![]() 与燃气量
与燃气量![]() 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,将点
,将点![]() 向右平移5个单位长度,得到点
向右平移5个单位长度,得到点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段![]() 恰有一个公共点,结合函数图象,求
恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
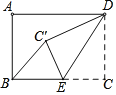
【题目】矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接DE,把△DCE沿DE折叠,使点C落在点C′处,当△BEC′为直角三角形时,BE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com