
【题目】小明参加学校组织的智力竞答活动,竞赛中有两道单选题完全不会.这两道单选题各有A.B.C三个选项,第一道单选答案是B.第二道单选答案是C.最终两道题小明随机各写了一个答案
(1)小明答对第一道题的概率是 .
(2)请用树状图或者列表求出小明两道题都答对的概率.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形A1B1C1D1,A2B2C2D2,A3B3C3D3…每个正方形四条边上的整点的个数.按此规律推算出正方形A10B10C10D10四条边上的整点共有______个.

查看答案和解析>>
科目:初中数学 来源: 题型:
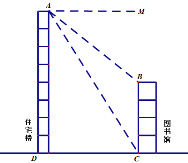
【题目】如图,小玲家在某24层楼的顶楼,对面新建了一幢28米高的图书馆,小玲在楼顶![]() 处看图书馆楼顶
处看图书馆楼顶![]() 处和楼底
处和楼底![]() 处的俯角分别是
处的俯角分别是![]() ,则两楼之间的距离是__________米.
,则两楼之间的距离是__________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)数轴上有A、B两点,若A点对应的数是﹣2,且A、B两点间的距离为3,则点B对应的数是________;
(2)已知线段AB=12cm,直线AB上有一点C,且BC=4cm,M是AC的中点,AM的长为________;
(3)已知∠AOB=3∠BOC,∠BOC=30°,则∠AOC=________;
(4)已知等腰三角形两边长为17、8,求三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣4,1),B(﹣2,3),C(﹣1,2).
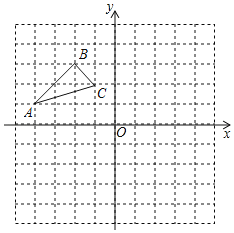
(1)画出△ABC关于原点O成中心对称的△A′B′C′,点A′,B′,C′分别是点A,B,C的对应点.
(2)求过点B′的反比例函数解析式.
(3)判断A′B′的中点P是否在(2)的函数图象上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(探索发现)
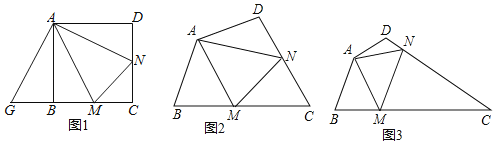
如图1,在正方形ABCD中,点M,N分别是边BC,CD上的点,∠MAN=45°,若将△DAN绕点A顺时针旋转90°到△BAG位置,可得△MAN≌△MAG,若△MCN的周长为8,则正方形ABCD的边长为 .
(2)(类比延伸)
如图2,在四边形ABCD中,AB=AD,∠BAD=120°,∠B+∠D=180°,点M,N分别在边BC,CD上的点,∠MAN=60°,请判断线段BM,DN,MN之间的数量关系,并说明理由.
(3)(拓展应用)
如图3,在四边形ABCD中,AB=AD=2,∠ADC=120°,点M,N分别在边BC,CD上,连接AM,MN,AN,△ABM是等边三角形,AM⊥AD于点A,∠DAN=15°,请直接写出△CMN的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
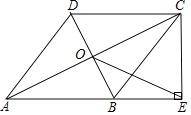
【题目】如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=![]() ,BD=2,求OE的长.
,BD=2,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
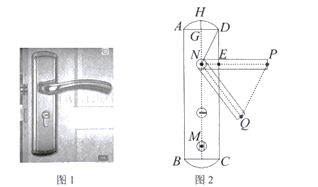
【题目】小明家的门框上装有一把防盗门锁(如图1)其平面结构图如图2所示,锁身可以看成由两条等弧![]() 和矩形
和矩形![]() 组成,
组成,![]() 的圆心是倒锁按钮点
的圆心是倒锁按钮点![]() .其中
.其中![]() 的弓高
的弓高![]()
![]() .当锁柄
.当锁柄![]() 绕着点
绕着点![]() 旋转至
旋转至![]() 位置时,门锁打开,此时直线
位置时,门锁打开,此时直线![]() 与
与![]() 所在圆相切,且
所在圆相切,且![]() 则
则![]() 的长度约为____________
的长度约为____________![]() .(结果精确到
.(结果精确到![]() ,参考数据:
,参考数据:![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
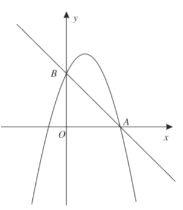
【题目】已知一次函数![]() 与二次函数
与二次函数![]() 的图象的一个交点坐标为
的图象的一个交点坐标为![]() ,另一个交点
,另一个交点![]() 在
在![]() 轴上,点
轴上,点![]() 为
为![]() 轴右侧抛物线上的一动点.
轴右侧抛物线上的一动点.
(1)求此二次函数的解析式;
(2)当点![]() 位于直线
位于直线![]() 上方的抛物线上时,求
上方的抛物线上时,求![]() 面积的最大值;
面积的最大值;
(3)当此抛物线在点![]() 与点
与点![]() 之间的部分(含点
之间的部分(含点![]() 和点
和点![]() )的最高点与最低点的纵坐标之差为9时,请直接写出点
)的最高点与最低点的纵坐标之差为9时,请直接写出点![]() 的坐标和
的坐标和![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com