
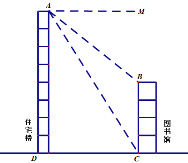
【题目】如图,小玲家在某24层楼的顶楼,对面新建了一幢28米高的图书馆,小玲在楼顶![]() 处看图书馆楼顶
处看图书馆楼顶![]() 处和楼底
处和楼底![]() 处的俯角分别是
处的俯角分别是![]() ,则两楼之间的距离是__________米.
,则两楼之间的距离是__________米.
科目:初中数学 来源: 题型:
【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成 5 组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
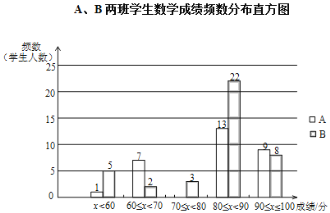
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A 班:80 80 82 83 85 85 86 87 87 87 88 89 89
B 班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,请写出表中 m、n的值____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年4月23日是我国第一个“全民阅读日”某校开展了“建设书香校园,捐赠有益图书”活动.我们在参加活动的所有班级中,随机抽取了一个班,已知这个班是八年级5班,全班共50名学生.现将该班捐赠图书情况的统计结果,绘制成如下两幅不完整的统计图.
请你根据以上信息,解答下列问题:
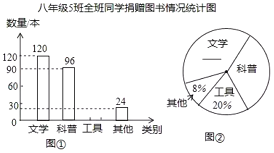
(1)补全上面的条形统计图和扇形统计图;
(2)求八年级5班平均每人捐赠了多少本书?
(3)若该校八年级共有800名学生,请你估算这个年级学生共可捐赠多少本书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六![]() 一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
一前夕,某幼儿园园长到厂家选购A、B两种品牌的儿童服装,每套A品牌服装进价比B品牌服装每套进价多25元,用2000元购进A种服装数量是用750元购进B种服装数量的2倍.
![]() 求A、B两种品牌服装每套进价分别为多少元?
求A、B两种品牌服装每套进价分别为多少元?
![]() 该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
该服装A品牌每套售价为130元,B品牌每套售价为95元,服装店老板决定,购进B品牌服装的数量比购进A品牌服装的数量的2倍还多4套,两种服装全部售出后,可使总的获利超过1200元,则最少购进A品牌的服装多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,若乙团队人数不超过40人,甲团队人数不超过80人,设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.
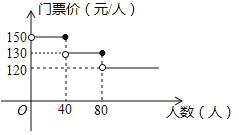
(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)该景区每年11月、12月为淡季,景区决定在这两个月实行门票打五折的优惠(打折期间不售团体票),以吸引大量游客,提高景区收入;景区经过调研发现,随着接待游客数的增加,景区的运营成本也随之增加,景区运营成本![]() (万元)与两个月游客总人数
(万元)与两个月游客总人数![]() (万人)之间满足函数关系式:
(万人)之间满足函数关系式:![]() ;两个月游客总人数
;两个月游客总人数![]() (万人)满足:
(万人)满足:![]() ,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润
,且淡季每天游客数基本相同;为了获得最大利润,景区决定通过网络预约购票的方式控制淡季每天游客数,请问景区的决定是否正确?并说明理由.(利润![]() 门票收入
门票收入![]() 景区运营成本)
景区运营成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线的顶点A的坐标为(1,4),抛物线与x轴相交于B、C两点,与y轴交于点E(0,3).
(1)求抛物线的表达式;
(2)已知点F(0,﹣3),在抛物线的对称轴上是否存在一点G,使得EG+FG最小,如果存在,求出点G的坐标;如果不存在,请说明理由.
(3)如图2,连接AB,若点P是线段OE上的一动点,过点P作线段AB的垂线,分别与线段AB、抛物线相交于点M、N(点M、N都在抛物线对称轴的右侧),当MN最大时,求△PON的面积.
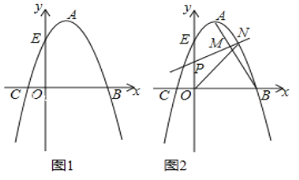
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
如图1,△ABC中,∠ACB=90°,点D在AB上,且∠BAC=2∠DCB,求证:AC=AD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作AE平分∠CAB,与CD相交于点E.
方法2:如图3,作∠DCF=∠DCB,与AB相交于点F.
(1)根据阅读材料,任选一种方法,证明AC=AD.
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4,△ABC中,点D在AB上,点E在BC上,且∠BDE=2∠ABC,点F在BD上,且∠AFE=∠BAC,延长DC、FE,相交于点G,且∠DGF=∠BDE.
①在图中找出与∠DEF相等的角,并加以证明;
②若AB=kDF,猜想线段DE与DB的数量关系,并证明你的猜想.
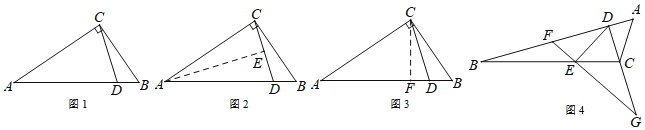
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加学校组织的智力竞答活动,竞赛中有两道单选题完全不会.这两道单选题各有A.B.C三个选项,第一道单选答案是B.第二道单选答案是C.最终两道题小明随机各写了一个答案
(1)小明答对第一道题的概率是 .
(2)请用树状图或者列表求出小明两道题都答对的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅社有100张床位,若每张床位每晚收费100元,床位可全部租出,若每张床位每晚收费提高20元,则减少10张床位租出;若每张床位每晚收费再提高20元,则再减少10张床位租出.以每次提高20元的这种方法变化下去,为了投资少而收入最多,每张床位每晚应提高( )
A.60元B.50元C.40元D.40元或60元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com