练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在过直线AB外一点P作直线AB的平行线时，可以按如下步骤进行：①在直线AB上任取两点C，D；②分别以点P，D为圆心，CD与PC为半径画弧，两弧交于点E；③作直线PE，则PE∥AB．在上面作图过程中，PE∥AB的依据是________．

    【答案】两组对边分别相等的四边形是平行四边形，平行四边形的两组对边分别平行

    【解析】

    由作图步骤可知PE=CD，DE=PC，根据两组对边分别相等的四边形是平行四边形，可得四边形PCDE是平行四边形，根据平行四边形两组对边分别平行即可得PE//AB．

    ∵分别以点P，D为圆心，CD与PC为半径画弧，两弧交于点E；

    ∴PE=CD，DE=PC，

    ∴四边形是平行四边形，

    ∵平行四边形的两组对边分别平行，

    ∴PE//AB，

    故答案为：两组对边分别相等的四边形是平行四边形，平行四边形的两组对边分别平行

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】2018年5月5日，中国邮政发行《马克思诞辰200周年》纪念邮票1套2枚（如图），这套邮票正面图案为：马克思像、马克思与恩格斯像，背面完全相同.发行当日，小宇购买了此款纪念邮票2套，他将2套邮票沿中间虚线撕开（使4枚形状、大小完全相同）后将4枚纪念邮票背面朝上放在桌面上，并随机从中抽出2张，则抽出的2张邮票恰好都是“马克思像”的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线的图像过点，顶点为

    求的值．

    点以点为旋转中心，顺时针旋转得到点，判断点是否落在抛物线上．

    第一象限内抛物线上有一点与相交于点，当时，求点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=﹣x2+bx+c经过点A、B、C，已知A（﹣1，0），C（0，3）．

    （1）求抛物线的解析式；

    （2）如图1，P为线段BC上一点，过点P作y轴平行线，交抛物线于点D，当△BDC的面积最大时，求点P的坐标；

    （3）如图2，抛物线顶点为E，EF⊥x轴于F点，M（m，0）是x轴上一动点，N是线段EF上一点，若∠MNC=90°，请指出实数m的变化范围，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】丁老师为了解所任教的两个班的学生数学学习情况，对数学进行了一次测试，获得了两个班的成绩（百分制），并对数据（成绩）进行整理、描述和分析，下面给出了部分信息．①A、B两班学生（两个班的人数相同）数学成绩不完整的频数分布直方图如下（数据分成 5 组：x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x≤100）：

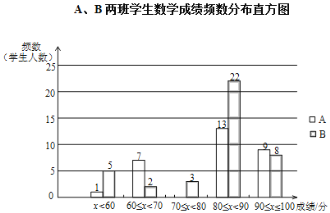
    ②A、B两班学生测试成绩在80≤x＜90这一组的数据如下：

    A 班：80 80 82 83 85 85 86 87 87 87 88 89 89

    B 班：80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89

    ③A、B两班学生测试成绩的平均数、中位数、方差如下：

    平均数

    中位数

    方差

    A班

    80.6

    m

    96.9

    B班

    80.8

    n

    153.3

    根据以上信息，请写出表中 m、n的值____________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，解决所提的问题：

    勾股定理a+b=c本身就是一个关于a，b，c的方程，我们知道这个方程有无数组解，满足该方程的正整数解（a，b，c）通常叫做勾股数组．关于勾股数组的研究我国历史上有非常辉煌的成就，根据我国古代数学书《周髀算经》记载，在约公元前1100年，人们就已经知道“勾广三、股修四、径隅五”（古人把较短的直角边称为勾，较长的直角边称为股，而斜边则为弦），即知道了勾股数组（3，4，5）．类似地，还可以得到下列勾股数组：（3，4，5），（5，12，13），（7，24，25），（9，40，41），…等等，这些数组也叫做毕达哥拉斯勾股数组．

    上述勾股数组的规律，可以用下面表格直观表示：

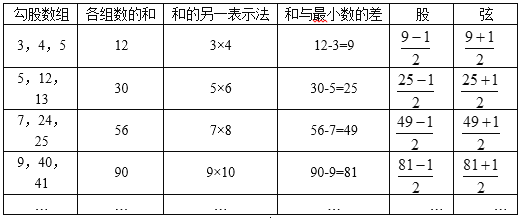
    观察分析上述勾股数组，可以看出它们具有如下特点：

    特点1：最小的勾股数的平方等于另两个勾股数的和；

    特点2：____________________________________．

    …

    学习任务：

    （1）请你再写出上述勾股数组的一个特点：________________；

    （2）如果n表示比1大的奇数，则上述勾股数组可以表示为（n，______，______）

    （3）请你证明（2）的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

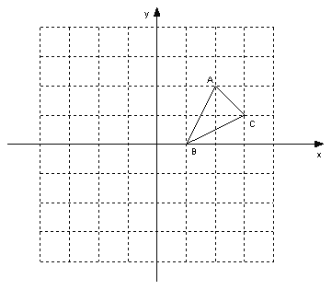
    【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1,0）

    （1）画出△ABC关于x轴对称的△A1B1C1，

    （2）画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2，

    （3）△A1B1C1与△A2B2C2成轴对称图形吗？若成轴对称图形，画出所有的对称轴并写出对称轴；

    （4）△A1B1C1与△A2B2C2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一艘轮船以每小时40海里的速度在海面上航行，当该轮船行驶到B处时，发现灯塔C在它的东北方向，轮船继续向北航行，30分钟后到达A处，此时发现灯塔C在它的北偏东75°方向上，求此时轮船与灯塔C的距离．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

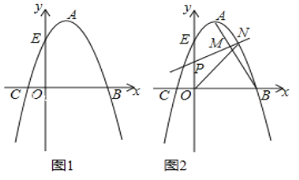
    【题目】如图1，抛物线的顶点A的坐标为（1，4），抛物线与x轴相交于B、C两点，与y轴交于点E（0，3）．

    （1）求抛物线的表达式；

    （2）已知点F（0，﹣3），在抛物线的对称轴上是否存在一点G，使得EG+FG最小，如果存在，求出点G的坐标；如果不存在，请说明理由．

    （3）如图2，连接AB，若点P是线段OE上的一动点，过点P作线段AB的垂线，分别与线段AB、抛物线相交于点M、N（点M、N都在抛物线对称轴的右侧），当MN最大时，求△PON的面积．

    查看答案和解析>>

    同步练习册答案