
【题目】如图,矩形ABCD中,AB=6,AD=8.动点E,F同时分别从点A,B出发,分别沿着射线AD和射线BD的方向均以每秒1个单位的速度运动,连接EF,以EF为直径作⊙O交射线BD于点M,设运动的时间为t.
(1)当点E在线段AD上时,用关于t的代数式表示DE,DM.
(2)在整个运动过程中,
①连结CM,当t为何值时,△CDM为等腰三角形.
②圆心O处在矩形ABCD内(包括边界)时,求t的取值范围,并直接写出在此范围内圆心运动的路径长.
【答案】(1)(1)ED=8﹣t,MD=![]() .(2)①t=
.(2)①t=![]() 或t=
或t=![]() 或t=
或t=![]() ;②0≤t≤
;②0≤t≤![]() ,圆心运动的路径长为
,圆心运动的路径长为![]()
【解析】
(1)在Rt△ABD中,依据勾股定理可求得BD的长,然后依据MD=EDcos∠MDE,cos∠MDE=cos∠ADB=![]() ,由此即可解决问题.
,由此即可解决问题.
(2)①可分为点E在AD上,点E在AD的延长线上画出图形,然后再依据MC=MD,CM=CD、DM=DC三种情况求解即可;
②当t=0时,圆心O在AB边上.当圆心O在CD边上时,过点E作EH∥CD交BD的延长线与点H.先求得DH的长,然后依据平行线分线段成比例定理可得到DF=DH,然后依据DF=DH列出关于t的方程,从而可求得t的值,故此可得到t的取值范围.
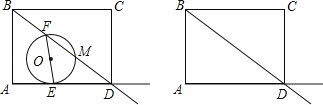
解:(1)如图1所示:连接ME.

∵AE=t,AD=8,
∴ED=AD-AE=8-t.
∵EF为⊙O的直径,
∴∠EMF=90°.
∴∠EMD=90°.
∴MD=EDcos∠MDE=![]() .
.
(2)①a、如图2所示:连接MC.
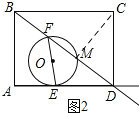
当DM=CD=6时,![]() =6,解得t=
=6,解得t=![]() ;
;
b、如图3所示:当MC=MD时,连接MC,过点M作MN⊥CD,垂足为N.

∵MC=MD,MN⊥CD,
∴DN=NC.
∵MN⊥CD,BC⊥CD,
∴BC∥MN.
∴M为BD的中点.
∴MD=5,即![]() =5,解得t=
=5,解得t=![]() ;
;
c、如图4所示:CM=CD时,过点C作CG⊥DM.

∵CM=CD,CG⊥MD,
∴GD![]() MD=
MD=![]() .
.
∵![]() ,
,
∴DG=![]() CD=
CD=![]() .
.
∴![]() =
=![]() .
.
解得:t=-1(舍去).
d、如图5所示:当CD=DM时,连接EM.
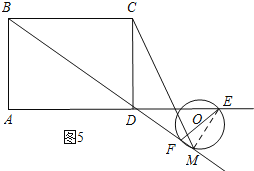
∵AE=t,AD=8,
∴DE=t-8.
∵EF为⊙O的直径,
∴EM⊥DM.
∴DM=EDcos∠EDM=![]() .
.
∴![]() =6,解得:t=
=6,解得:t=![]() .
.
综上所述,当t=![]() 或t=
或t=![]() 或t=
或t=![]() 时,△DCM为等腰三角形.
时,△DCM为等腰三角形.
②当t=0时,圆心O在AB边上.
如图6所示:当圆心O在CD边上时,过点E作EH∥CD交BD的延长线与点H.
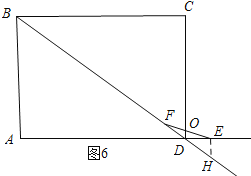
∵HE∥CD,OF=OE,
∴DF=DH.
∵DH=![]() =
=![]() ,DF=10-t,
,DF=10-t,
∴![]() =10-t.
=10-t.
解得:t=![]() .
.
综上所述,在整个运动过程中圆心O处在矩形ABCD内(包括边界)时,t的取值范围为0≤t≤![]() .
.
此时点O的运动路径为OO1的长度,如图:
过点O作OM⊥AB
当t=![]() 时,DE=
时,DE=![]() -8=
-8=![]()
∵EH∥CD,AB∥CD
∴EH∥AB
∴△DEH∽△DAB
∴![]() ,即
,即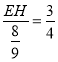 ,解得EH=
,解得EH=![]()
∴OD=![]() EH=
EH=![]()
由题意可知四边形ADOK是矩形
∴AK= OD =![]() ,OK=AD=8
,OK=AD=8
∴O1K= O1A- AK=![]()
在Rt△OKO1中,OO1=![]()
∴圆心运动的路径长为![]() .
.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用下面的折线统计图表示:(甲为实线,乙为虚线)
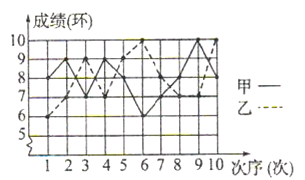
(1)依据折线统计图,得到下面的表格:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 |
| 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 |
| 10 |
其中![]() ________,
________,![]() ________;
________;
(2)甲成绩的众数是________环,乙成绩的中位数是________环;
(3)请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?
(4)该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
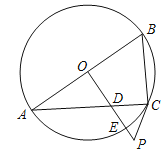
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级(1)班学生即将所穿校服型号情况进行摸底调查,并根据调查结果绘制如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
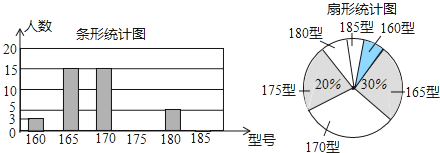
根据以上信息,解答下列问题:
(1)该班共有多少名学生?
(2)在条形统计图中,请把空缺部分补充完整;在扇形统计图中,请计算185型校服所对应的扇形圆心角的大小;
(3)求该班学生所穿校服型号的众数和中位数.如果该高中学校准备招收2000名高一新生,则估计需要准备多少套180型号的校服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,求作
,求作![]() 的外心
的外心![]() ,以下是甲、乙两同学的作法:对于两人的作法:
,以下是甲、乙两同学的作法:对于两人的作法:
甲:如图1,(1)作![]() 的垂直平分线
的垂直平分线![]() ;
;
(2)作![]() 的垂直平分线
的垂直平分线![]() ;
;
(3)![]() ,
,![]() 交于点
交于点![]() ,则点
,则点![]() 即为所求.
即为所求.
乙:如图2,(1)作![]() 的平分线
的平分线![]() ;
;
(2)作![]() 的垂直平分线
的垂直平分线![]() ;
;
(3)![]() ,
,![]() 交于点
交于点![]() ,则点
,则点![]() 即为所求.
即为所求.
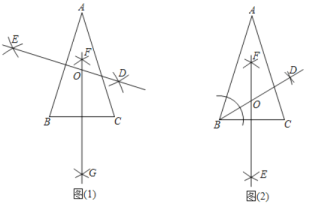
对于两人的作法,正确的是( )
A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一副直角三角板如图放置,其中BC=6,EF=8,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为_____.
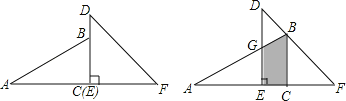
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2= ![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() =( )
=( )
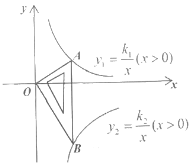
A.-3 B.3 C.![]() D.-
D.- ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com