练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

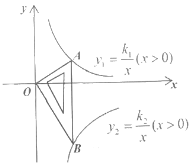
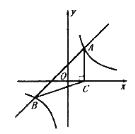
    【题目】如图所示是一块含30°，60°，90°的直角三角板，直角顶点O位于坐标原点，斜边AB垂直于x轴，顶点A在函数y1=（x>0）的图象上，顶点B在函数y2= （x>0）的图象上，∠ABO=30°，则=（ ）

    A.-3 B.3 C. D.-

    【答案】A

    【解析】

    根据30°角所对的直角边等于斜边的一半，和勾股定理，设出适当的常数，表示出其它线段，从而得到点A、B的坐标，表示出k1、k2，进而得出k2与k1的比值．

    如图，设AB交x轴于点C，又设AC=a.

    ∵AB⊥x轴 ∴∠ACO=90°

    在Rt△AOC中，OC=AC·tan∠OAB=a·tan60°=a

    ∴点A的坐标是（a，a）

    同理可得 点B的坐标是（a，-3a）

    ∴k1=a×a=a2 ， k2=a×（-3a）=-3a

    ∴.

    故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

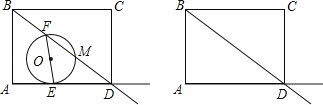
    【题目】如图，矩形ABCD中，AB＝6，AD＝8．动点E，F同时分别从点A，B出发，分别沿着射线AD和射线BD的方向均以每秒1个单位的速度运动，连接EF，以EF为直径作⊙O交射线BD于点M，设运动的时间为t．

    （1）当点E在线段AD上时，用关于t的代数式表示DE，DM．

    （2）在整个运动过程中，

    ①连结CM，当t为何值时，△CDM为等腰三角形．

    ②圆心O处在矩形ABCD内（包括边界）时，求t的取值范围，并直接写出在此范围内圆心运动的路径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

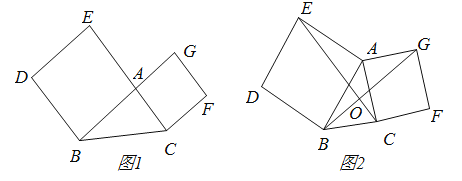
    【题目】如图1,正方形和正方形, 连接,当时， 与的关系是？

    如图2,将正方形绕点顺时针旋转，中结论是否仍然成立?若成立，请给出证明:若不成立，请说明理由;

    已知，在旋转过程中，若直线平分,请画出相应的图形，并写出其中一种情形时长的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD 中，对角线 AC 与 BD 相交于点 O ，点 E ， F 分别为 OB ， OD 的中点，延长 AE 至 G ，使 EG ＝AE ，连接 CG ．

    （1）求证： △ABE≌△CDF ；

    （2）当 AB 与 AC 满足什么数量关系时，四边形 EGCF 是矩形？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明将小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度y(m)与它的飞行时间x(s)满足二次函数关系，y与x的几组对应值如下表所示：

    x(s)

    0

    0.5

    1

    1.5

    2

    …

    y(m)

    0

    8.75

    15

    18.75

    20

    …

    (Ⅰ)求y关于x的函数解析式(不要求写x的取值范围)；

    (Ⅱ)问：小球的飞行高度能否达到22m？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中华文明，源远流长，中华汉字，寓意深广.为传承中华优秀传统文化，某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩，学校德育处随机抽取了其中200名学生的成绩作为样本进行统计，制成如下不完整的统计图表：

    成绩x（分）分数段

    频数（人）

    频率

    50≤x<60

    10

    0.05

    60≤x<70

    30

    0.15

    70≤x<80

    40

    0.2

    80≤x<90

    m

    0.35

    90≤x<100

    50

    n

    频数分布直方图

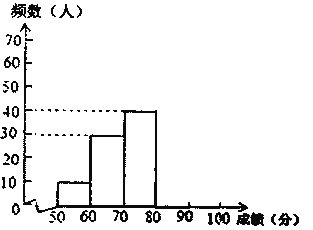
    根据所给的信息，回答下列问题：

    （1）m=________；n=________；

    （2）补全频数分布直方图；

    （3）这200名学生成绩的中位数会落在________分数段；

    （4）若成绩在90分以上（包括90分）为“优”等，请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列方程（组）或不等式组：

    （1）解方程组

    （2）解分式方程+1＝：

    （3）求不等式组的整数解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某种洗衣机在洗涤衣服时，经历了进水、清洗、排水、脱水四个连续的过程，其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示．根据图象解答下列问题：

    (1)洗衣机的进水时间是多少分钟？清洗时洗衣机中水量为多少升？

    (2)已知洗衣机的排水速度为每分钟19升．

    ①求排水时洗衣机中的水量y(升)与时间x(分钟)与之间的关系式；

    ②如果排水时间为2分钟，求排水结束时洗衣机中剩下的水量．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数的图象与反比例函数（为常数，）的图象交于，两点，点的坐标为（1，2）．

    （1）求两个函数的表达式和点坐标；

    （2）过点作轴的垂线交轴于点，求的面积；

    （3）根据图象直接写出当时，自变量的取值范围．

    查看答案和解析>>

    同步练习册答案