
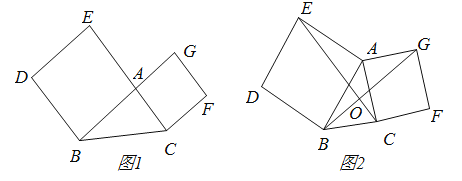
【题目】![]() 如图1,正方形
如图1,正方形![]() 和正方形,
和正方形,![]() 连接
连接![]() ,当
,当![]() 时,
时, ![]() 与
与![]() 的关系是?
的关系是?
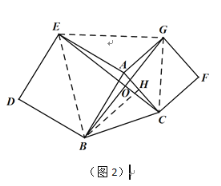
![]() 如图2,将正方形
如图2,将正方形![]() 绕点
绕点![]() 顺时针旋转,
顺时针旋转,![]()
![]() 中结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由;
中结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由;
![]() 已知
已知![]() ,在旋转过程中,若直线
,在旋转过程中,若直线![]() 平分
平分![]() ,请画出相应的图形,并写出其中一种情形时
,请画出相应的图形,并写出其中一种情形时![]() 长的思路.
长的思路.
【答案】(1)BG⊥CE,BG=CE;(2)(1)中结论仍然成立,理由见解析;(3)见解析
【解析】
(1)由题干提供的已知条件直接得到答案,
(2)利用正方形的性质证明△CAE≌△GAB,得到BG=CE,∠CEA=∠GBA,再利用三角形内角和可得答案,
(3)当点O在EC上时,连接BE,CG,利用已证明的结论BG⊥CE,BG=CE,结合已知条件直线![]() 平分
平分![]() 与正方形的性质,利用勾股定理列方程组即可得到答案.
与正方形的性质,利用勾股定理列方程组即可得到答案.
(1)BG⊥CE,BG=CE;
(2)(1)中结论仍然成立
证明:∵正方形ABDE和正方形ACFG,
∴AE=AB,AC=AG,∠EAB=∠CAG=90°,
∴∠EAC=∠BAG,
在△CAE和△BAG中,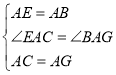 ,
,
∴△CAE≌△GAB,
∴BG=CE,∠CEA=∠GBA,
又∠1=∠2
∴∠EAB=∠EOB=90°,
∴BG⊥CE;
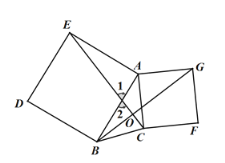
(3)①当点O在EC上时,
方法一:如图1,连接BE,CG,
设BO=GO=x,OC=y,则OE=2x-y,
利用勾股定理建立方程组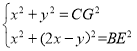 ,
,
求出x,得CE长.
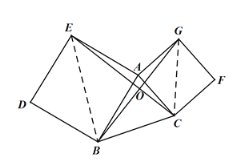
(图1)
方法二:如图2,连接BE,CG,EG,作BH⊥AC于点H,
先求CG,得BC的长,再求S△ABC,
然后证明S△ABC=S△AEG,利用面积法建立方程:
![]() ,求得CE长;
,求得CE长;
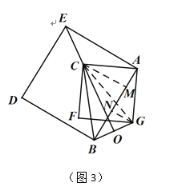
②如图3,当点O在EC延长线上时,
连接CG,作CM⊥AB于点M,GN⊥AB于点N,
由①知BC长,利用勾股定理建立方程组可求CM长
(或结合①BH长利用面积法求CM长),进而求AM长,
证△ACM≌△GAN,得AN,GN长,于是得到BN长,
再利用勾股定理求得BG长,得CE长.


科目:初中数学 来源: 题型:
【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格也相同).若购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元,购买
元,购买![]() 个篮球和
个篮球和![]() 个足球共需
个足球共需![]() 元.
元.
(1)购买一个篮球、一个足球各需多少元?
(2)根据该中学的实际情况,需从体育用品商店一次性购买篮球和足球共![]() 个.要求购买总金额不能超过
个.要求购买总金额不能超过![]() 元,则最多能购买多少个篮球?
元,则最多能购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一副直角三角板如图放置,其中BC=6,EF=8,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为_____.
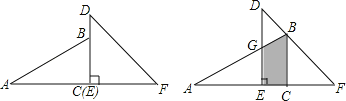
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣9ax+18a的图象与x轴交于A,B两点(A在B的左侧),图象的顶点为C,直线AC交y轴于点D.
(1)连接BD,若∠BDO=∠CAB,求这个二次函数的表达式;
(2)是否存在以原点O为对称轴的矩形CDEF?若存在,求出这个二次函数的表达式,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象交x轴于点A,B(点A在点B的左侧).
的图象交x轴于点A,B(点A在点B的左侧).
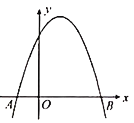
(1)求点A,B的坐标,并根据该函数图象写出y≥0时x的取值范围;
(2)把点B向上平移m个单位得点B1.若点B1向左平移n个单位,将与该二次函数图象上的点B2重合;若点B1向左平移(n+6)个单位,将与该二次函数图象上的点B3重合.已知m>0,n>0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() ,垂足为
,垂足为![]() ,且交
,且交![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,延长
,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() .有如下结论:①
.有如下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .上述结论中,所有正确结论的序号是( )
.上述结论中,所有正确结论的序号是( )
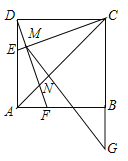
A. ①②B. ①③C. ①②③D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2= ![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() =( )
=( )
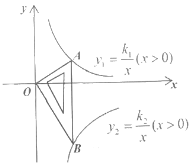
A.-3 B.3 C.![]() D.-
D.- ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com